filmov
tv
Solving A Nice Rational Equation | Math Olympiads
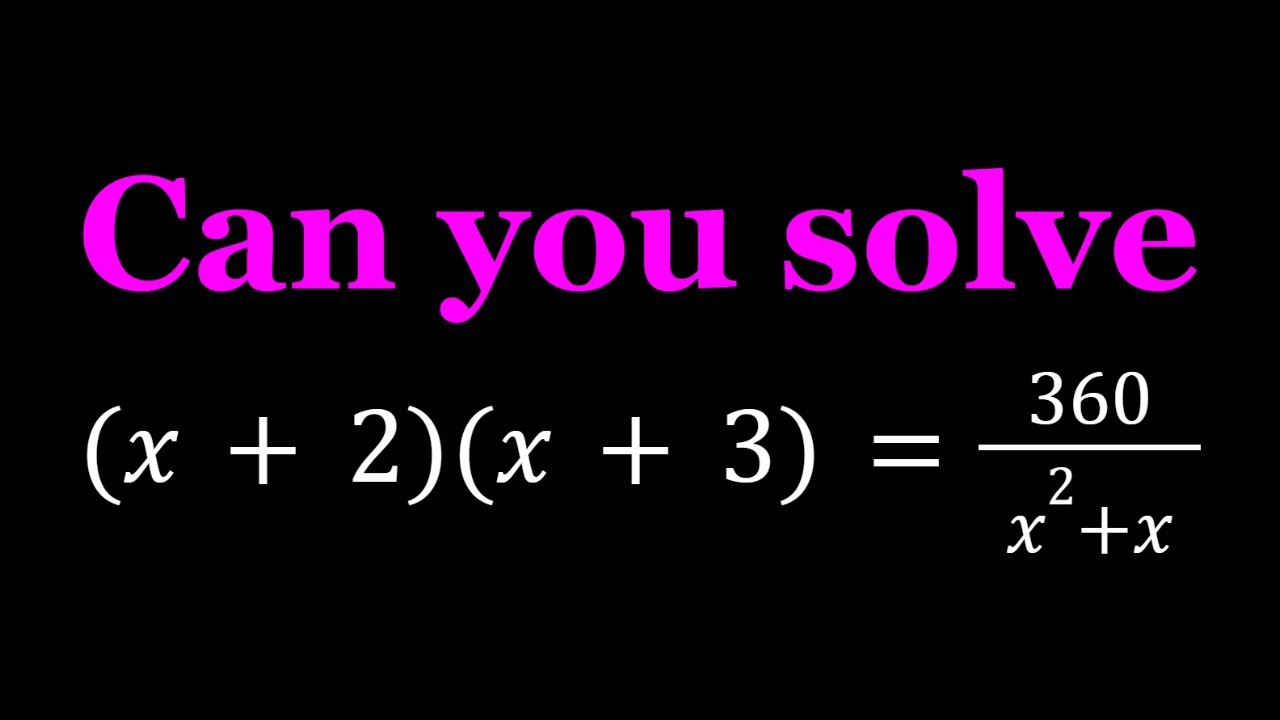
Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts)
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
😲 The Infamous Quartic Formula:🤩
#ChallengingMathProblems #PolynomialEquations #Polynomials
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
😲 The Infamous Quartic Formula:🤩
#ChallengingMathProblems #PolynomialEquations #Polynomials
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Solving Rational Equations
Solving Rational Equations Easier Method
Solving A Cool Rational Equation
Solving Rational Equations Tutorial
A Nice Rational Equation | Two Methods
How To Solve Rational Equations In Easy Steps! Gen Math and Grade 8
Solving a Nice Rational Equation in Two Ways
Solving Rational Equations
Why Solving a Rational Equation is Tricky!
Math tutorial for solving rational equations
Solving a rational Equation
Solving a rational Equation
Ex: Solve a Rational Equation
A Nice Rational Equation | #algebra
A Rational Equation
Solving a rational equation with two solutions
Solving a Nice Rational Equation using Substitutions | Math Olympiad
Solving A Nice Rational Equation | Math Olympiads
Solve a Rational Equation with two solutions
How To Solve A Nice Rational Equation | Math Olympiads
Solving a rational equation by factoring
Solving a rational equation that requires factoring (Precalculus)
Solving a rational Equation
Solving Rational Equations
Комментарии
 0:11:03
0:11:03
 0:04:33
0:04:33
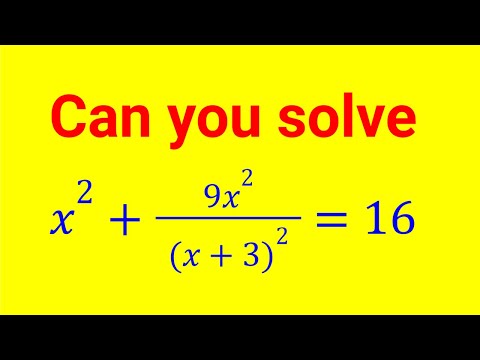 0:09:17
0:09:17
 0:04:22
0:04:22
 0:09:24
0:09:24
 0:12:06
0:12:06
 0:09:53
0:09:53
 0:12:57
0:12:57
 0:08:13
0:08:13
 0:06:32
0:06:32
 0:05:33
0:05:33
 0:07:12
0:07:12
 0:04:29
0:04:29
 0:09:32
0:09:32
 0:08:20
0:08:20
 0:08:50
0:08:50
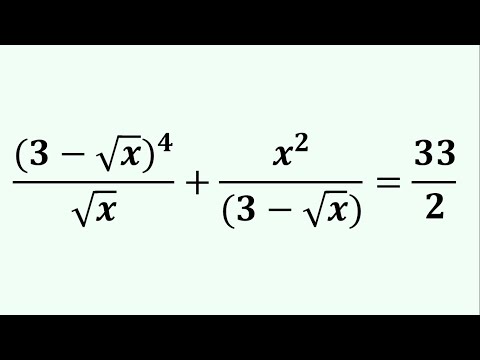 0:15:50
0:15:50
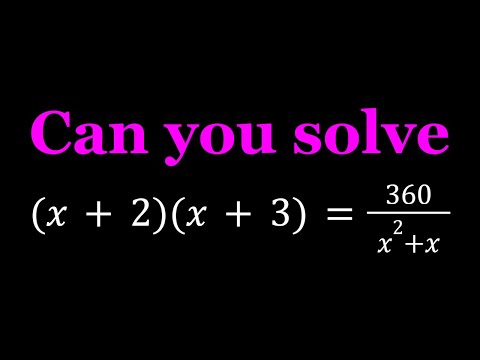 0:10:44
0:10:44
 0:01:23
0:01:23
 0:10:07
0:10:07
 0:08:54
0:08:54
 0:06:17
0:06:17
 0:02:56
0:02:56
 0:03:03
0:03:03