Law of Cosines (Trigonometry to Solve an Oblique Triangle SSS, SAS and Proof Worked Out)

Показать описание

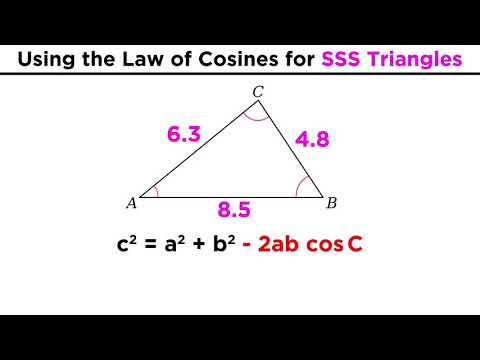
In this video we will be going over the trigometric law of cosines. It is used to solve an oblique triangle or triangle without a right angle. It can be used when given all three sides lengths of an oblique triangle or side length shared angle and side lenght. I have listed on this slide to the left all forms of the law of cosines to solve for each unsolved side or angle…
So now lets prove the law of cosines. To help illustrate this proof I have a triangle with angles designated with a capital A B and C and side length directly across from the angles designated with lower case a b and d.
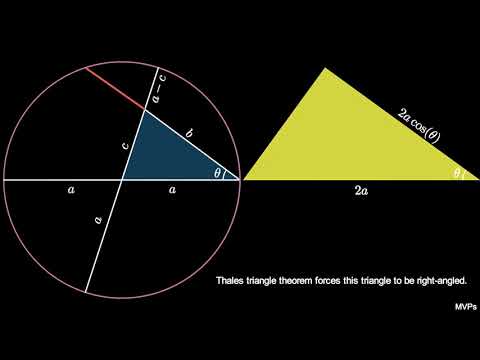
We will be drawing a line in the center of this triangle to make 2 right triangle. This line is perpendicular of side C and connects at point of angle c
Now we will overlay a x and y axis over the triangle with the orgin being at the A angle point so it is 0,0 here
At the b angle point we will designate it with an x length of side length c of the triangle and a y height of 0
At the c angle we will designate this with a purple x and a orange y because these values are not yet known. Notice that the y and x make up the height and length of one of the right triangles formed by making a line connecting C angle point at a 90 degree angle or perpendicular to the c side of the triangle
Now lets use what we are given to find side length A.
Recall that to find the distance from one point to another we can use the Pythagorean theorem also known when working with coordinates as the distance formula. For the right triangle to the right of the perpenidular line the length is side length x- c and the height is simply y – 0 which reduces to y. Note I used point 2 as x,y and point 1 as c, zero in the distance formula this is why it is x-c and not c –x
Taking the square of both sides we are left with a squared being equal to x – c squared plus y – 0 squared.
So now we need to find a way to relate x and y to the side lengths and angles of the oblique triangle. We can do this by using the way to solve right triangle soh cah toa. We will be concentrating on the right triangle left of the perpendicular line. So we can redefine x as the adjacent side and use a rearranged CAH of b side length times the cosine of angle A and we can redefine y as the opposite side and use a rearranged SOH of b side length times the sine of angle A
Plugging those values into the above equation we are left with this equation.
Now we must use foil method to change the form of the binomial side length b cosine of angle a minus c squared
Doing so we are left with this equation. Notice that we can factor out b squared to make the equation more reducable.
Completing this we are left with b squared time parthesis cosine squared of angle a plus sine squared angle a parthesis.
Recall that cosine squared of angle plus sine squared of the same angle is a trigometric identity equal to one
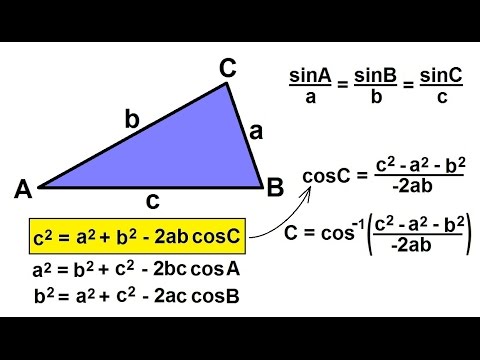
Plugging that one into the equation and doing a little reranging we are left with a squared equals b squared plus c squared minus 2 b c times the cosine of angle A. This is one of the forms of the law of cosines. You can find the other forms by completing the same process for other side lengths You might want to pause here to take this all in
Looking at the law of cosines of the left we notice that the last 3 are simply the above 3 reranged so that the angle is on one side.
Here is a form of the equations further reranged to allow you to simply plug and chug to solve your desired problem. I have also listed a triangle with all of the values listed so you can practice solving for one of these variables using these equations as practice. Pause here. I figure it would be to daunting to listen to me state out all of the filled in equations.

Disclaimer
These videos are intended for educational purposes only (students trying to pass a class) If you design or build something based off of these videos you do so at your own risk. I am not a professional engineer and this should not be considered engineering advice. Consult an engineer if you feel you may put someone at risk.