filmov
tv
Deriving the Law of Cosines With Geometric Algebra

Показать описание
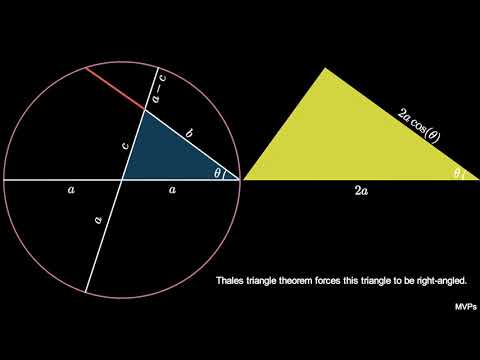
In this short, I show a quick derivation of the law of cosines using geometric algebra.
I thought I would try YouTube shorts out, so I'm planning on making one a week. This only took me several hours to make, so it shouldn't interfere with my main videos too much. Look forward to seeing more of these in the future!
Patreon Supporters:
Christoph Kovacs
David Johnston
Jason Killian
LoganMP
p11
Richard Penner
Rosario
I thought I would try YouTube shorts out, so I'm planning on making one a week. This only took me several hours to make, so it shouldn't interfere with my main videos too much. Look forward to seeing more of these in the future!
Patreon Supporters:
Christoph Kovacs
David Johnston
Jason Killian
LoganMP
p11
Richard Penner
Rosario
Law Of Cosines I (visual proof)
Law Of Cosines II (visual proof)
Proof of the cosine rule
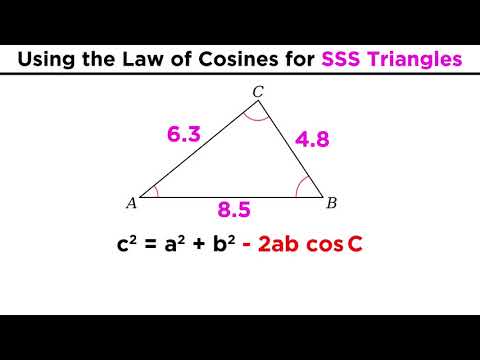
Law of Cosines, Finding Angles & Sides, SSS & SAS Triangles - Trigonometry
Proof of the Cosine Rule
Deriving the Law of Cosines With Geometric Algebra
Deriving The Law of Cosines [8.3-1]
The Law of Cosines
Deriving the Law of Cosines
Derivation of the Law of Cosines
The Cosine Law - Nerdstudy
Deriving the Law of Sines and Cosines
Law of Cosines Derivation
Deriving the Law of Cosines
Deriving the Law of Cosines
Trigonometry - Deriving the Law of Cosines
Deriving the Law of Cosines pg 112
HOW TO DERIVE SINE LAW AND COSINE LAW?
Deriving the Law of Cosines
Deriving the Law of Cosines
Law of Sines Visual Proof
Classic math proofs of the law of sine and the law of cosine
Deriving Spherical Law of Cosines
Deriving Law of Cosines
Комментарии
 0:02:31
0:02:31
 0:02:42
0:02:42
 0:06:07
0:06:07
 0:10:18
0:10:18
 0:08:10
0:08:10
 0:00:31
0:00:31
 0:07:09
0:07:09
 0:04:38
0:04:38
 0:04:44
0:04:44
 0:03:28
0:03:28
 0:05:44
0:05:44
 0:09:00
0:09:00
 0:04:16
0:04:16
 0:10:55
0:10:55
 0:10:01
0:10:01
 0:12:02
0:12:02
 0:09:23
0:09:23
 0:10:20
0:10:20
 0:15:12
0:15:12
 0:16:07
0:16:07
 0:02:58
0:02:58
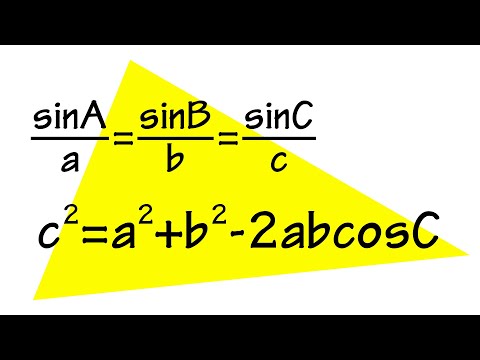 0:11:11
0:11:11
 0:15:17
0:15:17
 0:05:58
0:05:58