filmov
tv
Proof of the law of cosines

Показать описание
Using the Pythagorean theorem to prove the law of cosines.
#manim
#manim
Law of Sines Visual Proof
Law Of Cosines I (visual proof)
Law Of Cosines II (visual proof)
C.I.A. PROOF of The Law of Thought Transmission | Law of Assumption #manifestation #subconsciousmind
Proof of law of conservation of energy by taking the example of freely falling body #shorts
Proof the Law of Assumption Works! - Neville Goddard
LAW OF ATTRACTION - Proof That It Works
PROOF LAW OF ASSUMPTION WORKS🤯🤯 #shorts #lawofassumption #manifestation
INSTANT PANIC Hits WNBA After PROOF Referees TARGETING Caitlin Clark!
Simple PROOF that The Law of Attraction Works!
The Proof of Law of Karma and Rebirth - A MUST Watch Past-Life Story | Swami Mukundananda
PROOF That The Law Of Attraction WORKS 😱💰 - @JordanPlatten
Law of Sines Proof
Law of Attraction Proof: Watch These People Manifest the Impossible (Hindi)
What Exactly IS a Burden of Proof?
Proof of the cosine rule
Proof of the sine rule
The Law of Sines - Formula, Examples & Proof - [2-20-7]
A proof of the weak law of large numbers
Abraham Hicks - Law Of Attraction PROOF
Steve Harvey - Law of Attraction Proof (Full Guide to Manifest Success)
The Cosine Rule (1 of 3: Proof of the Formula)
Proof of the Cosine Rule
Law of Cosines - Formula, Examples & Proof - [2-20-4]
Комментарии
 0:02:58
0:02:58
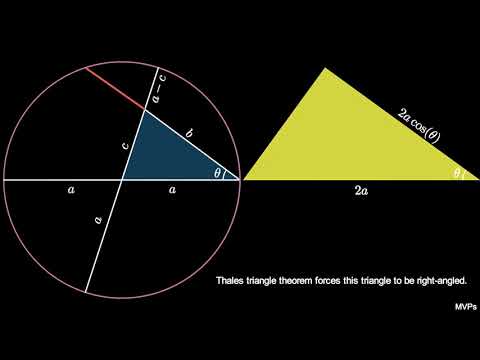 0:02:31
0:02:31
 0:02:42
0:02:42
 0:04:48
0:04:48
 0:00:07
0:00:07
 0:06:13
0:06:13
 0:07:15
0:07:15
 0:00:34
0:00:34
 0:02:09
0:02:09
 0:05:11
0:05:11
 0:19:24
0:19:24
 0:00:35
0:00:35
 0:00:34
0:00:34
 0:09:05
0:09:05
 0:00:52
0:00:52
 0:06:07
0:06:07
 0:04:11
0:04:11
 0:32:51
0:32:51
 0:04:04
0:04:04
 0:14:10
0:14:10
 0:49:23
0:49:23
 0:13:24
0:13:24
 0:08:10
0:08:10
 0:36:51
0:36:51