filmov
tv
Length Contraction Explained

Показать описание
Relativity is the idea that time and space can behave differently depending on your perspective. It is notoriously difficult to understand, but in this series, I explain the methods that helped me understand it to the best of my ability. This episode covers length contraction, where the lengths of objects change depending on velocity.
Intro Song: Chopin's Nocturne op 9 no 2, performed by Frank Levy
Outro Song: Tchaikovsky's Waltz of the Flowers, from youtube's media library
Intro Song: Chopin's Nocturne op 9 no 2, performed by Frank Levy
Outro Song: Tchaikovsky's Waltz of the Flowers, from youtube's media library
Special Relativity Part 3: Length Contraction
Length contraction: the real explanation
Length Contraction and Time Dilation | Special Relativity Ch. 5
Length Contraction is NOT an Illusion!
Length Contraction | Physics with Professor Matt Anderson | M29-01
I Never Understood Why Space Shrinks as You Approach Light Speed... Until Now
Length Contraction Explained
How Are Time Dilatation and Length Contraction Connected
E5 - Length Contraction Explained. Ask Us Whatever.
Is Length Contraction Real? The Genuine answer (Special Relativity)
What is Length Contraction?
Length Contraction (Special Theory of Relativity)
Special Relativity: Crash Course Physics #42
Special Relativity
How Special Relativity Makes Magnets Work
5 / How lengths get shorter in special relativity
Time Dilation and Length Contraction | Special Relativity
Time Dilation - Einstein's Theory Of Relativity Explained!
Time Dilation & Theory Of Relativity Simplified
Light Speed and Length Contraction in Einstein's Relativity #astrophysics
Length Contraction and Special Relativity
What is Length Contraction? (Thought Experiment)
Einstein's twin paradox explained - Amber Stuver
Special Relativity: Length Contraction
Комментарии
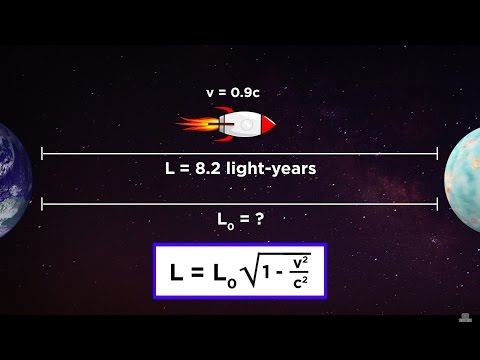 0:06:02
0:06:02
 0:11:23
0:11:23
 0:07:17
0:07:17
 0:10:19
0:10:19
 0:04:32
0:04:32
 0:18:57
0:18:57
 0:15:03
0:15:03
 0:05:40
0:05:40
 0:04:37
0:04:37
 0:06:46
0:06:46
 0:05:44
0:05:44
 0:19:54
0:19:54
 0:08:59
0:08:59
 0:12:59
0:12:59
 0:04:19
0:04:19
 0:05:02
0:05:02
 0:10:03
0:10:03
 0:08:06
0:08:06
 0:01:01
0:01:01
 0:01:01
0:01:01
 0:06:45
0:06:45
 0:11:47
0:11:47
 0:06:16
0:06:16
 0:08:43
0:08:43