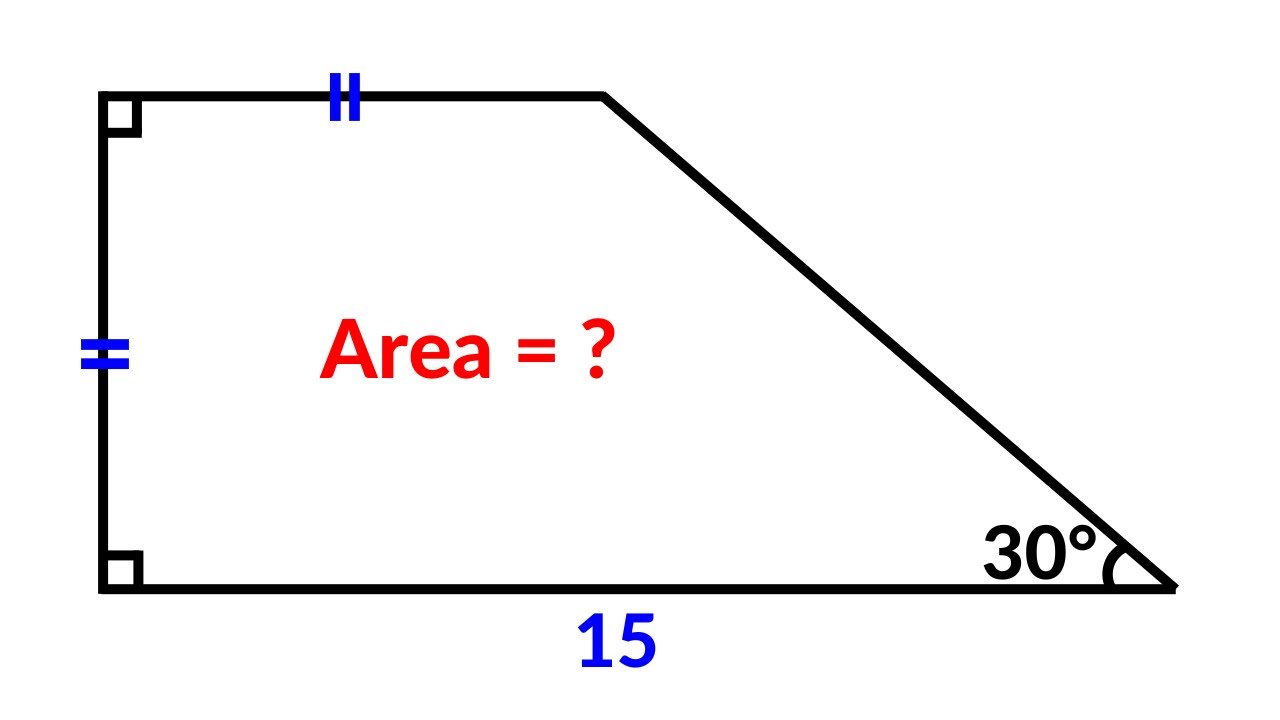
A Very Nice Geometry Problem | Find the area of the Trapezium (Trapezoid)

GET MY EBOOKS
•••••••••••••••••••••••

OTHER CHAPTERS : COMING SOON.....
--------------------------------------------------------------------------------

Join the channel to become a member

[prossvay]

Let AD=DE=BE=BA=a
(E on CD)
So CE=15-a
tan(30)=BE/CE=a/15-a
a=(15√3-15)/2
So area of the

[thomasharding]

Tan 30 degrees => Adjacent side = 1.73X => 2.73X = 15 => X = 5.49 Square area = 30.14 square cm. Adj. side of 30 degree angle = 9.50 and Opp side = 5.49 Area of Rt. Triangle = product of the two sides divided by 2. = (9.48 x 5.48) / 2 = 25.98 square cm. Area of triangle + area of square = 25.98 + 30.14 = 56.12 square cm.

[michaeldoerr]

I really needed that refresher on calculating the area of a trapezoid. The area is 225/4 units squared!

[lasalleman]

Set up a triangle out of BCD. Angle at C is 30 degrees, Angle at D is 45 degrees. Base is 15. Area is 41.17. Height is 5.49. Thus line AD is 5.49, as is line AB. Area of the triangle is thus 15.07. Total area of trapezoid is thus 56.24.

[ناصريناصر-سب]

We have the shape AD/(CD-AB)=tan(30) and from it, assuming AB=x, x/(15-x)=√3/3, from it x=(15√3-15)/2, from it, the area of ABCD is 225/4.

[alexniklas]

I decided the same
S= 225/4= 56, 25
Thanks sir😊

[sorourhashemi]

Thanks. Easy. BC=2X, so X^2+(15-X)^2=2X^2===>X=5.49, area= 56.24

[jimlocke]

"Thinking outside the box", extend AD and BC until they meet, and call the intersection point E. ΔEAB and ΔEDC are 30°-60°-90° right triangles, therefore their short sides are 1/√3 times as long as the long sides. ED = CD/(√3) = 15/√3. Let AB = AD = x, then EA = x/√3. Then, ED = EA + AD = x + x/√3 = x(1 + 1/√3), but ED also = 15/√3, so x(1 + 1/√3) = 15/√3, x(√3 + 1) = 15 and x = (15)/(1 + √3). EA = x/√3 = (15/√3)/(1 + √3). The area of the trapezium (trapezoid) = area (ΔEAB - ΔEDC). Area ΔEAB = (1/2)(15)(15/√3) = (225)/(2√3) = (225√3)/6. Area ΔEDC = (1/2)((15/√3)/(1 + √3))(15/(1 + √3)) = 225/((2√3)(1 + √3)²) = (225/((2√3)(4 + 2√3)) = (225)/((4√3)(2 + √3)). Multiply by (2 - √3)/(2 - √3) and note that (2 + √3)(2 - √3) = 4 - 3 = 1: Area ΔEDC = (225/4)(2 - √3)/(√3). Multiply by (√3)/(√3): (225/4)(2√3 - 3)/(3) = (225√3)/6 - 225/4. Trapezium (trapezoid) area = area (ΔEAB - ΔEDC) = (225√3)/6 - ((225√3)/6 - 225/4) = 225/4, as Math Booster also found.

[murdock]

φ = 30° → sin⁡(3φ) = 1; ∎ABED → AB = BE = DE = AD = k; ∆ BEC → BE = k
CE = 15 - k; BC = 2k; ECB = φ → tan⁡(φ) = √3/3 = k/(15 - k) → k = (15/2)(√3 - 1) →
area ABCD = (k/2)(k + 15) = (15/4)(√3 - 1)(15/2)(√3 + 1) = (15/2)^2

[jairoeveliogordillomarin]

Aplicando ley de senos en triángulo rectángulo 60° y 30°.
X= 5.49 u.
Área trapecio= 56.24 u².

[RealQinnMalloryu]

(15)^2=225 1.3^5 1.3^1 3^1 (ADBC ➖ 3ADBC+1).