filmov
tv
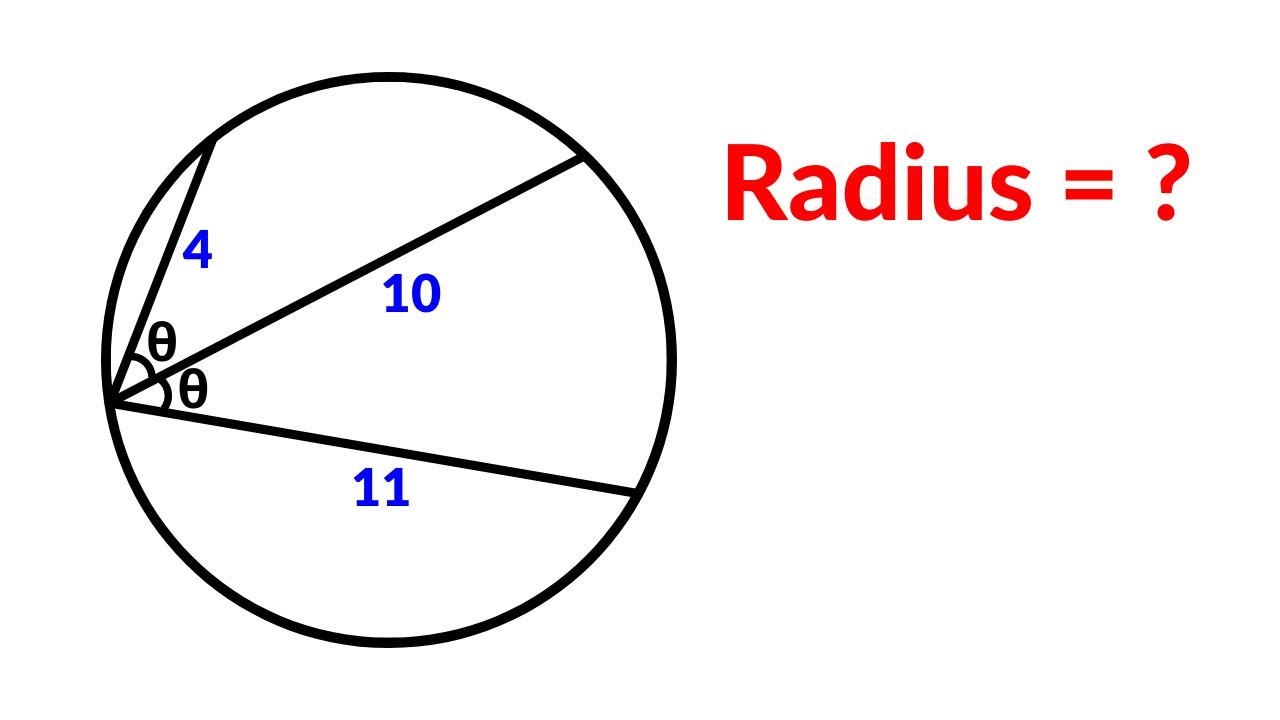
France Math Olympiad | A Very Nice Geometry Problem
Показать описание
GET MY EBOOKS
•••••••••••••••••••••••
OTHER CHAPTERS : COMING SOON.....
--------------------------------------------------------------------------------
Join the channel to become a member
•••••••••••••••••••••••
OTHER CHAPTERS : COMING SOON.....
--------------------------------------------------------------------------------
Join the channel to become a member
France - Math Olympiad Question | An Algebraic Expression | You should be able to solve this!
France Math Olympiad | A Very Nice Geometry Problem
France - Math Olympiad Problem
France - Math Olympiad Question | Be Careful!
France| Math Olympiad question #math#matholympiad
France Math Olympiad Problem | A Very Nice Geometry Challenge
France Math Olympiad Question | You should know this trick!
France - Math Olympiad Problem | Be Careful!
France Maths Olympiad question || maths olympiad algebra problem
France Math Olympiad Problem | Best Math Olympiad Problems | Geometry Problem
France - Math Olympiad Question
France | Can you solve this ? | Math Olympiad a=? b= ? c=? #maths #mamtamaam #olympiad
France - Math Olympiad Question | Calculus
Solving Simultaneous Equations Made Easy: France Math Olympiad Trick
France - Math Olympiad Challenge | Best Trick
France | Can you solve | Math Olympiad
France| A nice math Olympiad question #maths #matholympiad
France | Junior Math Olympiad | A Nice Algebra Problem | Simplify?
Luxembourg - Math Olympiad Question | You should know this trick
France - Math Olympiad Question | Calculus
France - Math Olympiad Question | Calculus
France - Math Olympiad Question | Calculus
France | Can you solve this ? | Math Olympiad | X=? & Y=? 👇
France math olympiad problem | You should know this trick |
Комментарии
 0:08:40
0:08:40
 0:12:37
0:12:37
 0:05:03
0:05:03
 0:15:49
0:15:49
 0:10:23
0:10:23
 0:12:24
0:12:24
 0:04:02
0:04:02
 0:12:11
0:12:11
 0:04:44
0:04:44
 0:12:25
0:12:25
 0:04:00
0:04:00
 0:03:03
0:03:03
 0:02:51
0:02:51
 0:03:41
0:03:41
 0:12:23
0:12:23
 0:02:26
0:02:26
 0:08:48
0:08:48
 0:14:39
0:14:39
 0:02:51
0:02:51
 0:02:39
0:02:39
 0:02:57
0:02:57
 0:02:11
0:02:11
 0:08:27
0:08:27
 0:02:29
0:02:29