filmov
tv
Boundary Conditions Replace Initial Conditions
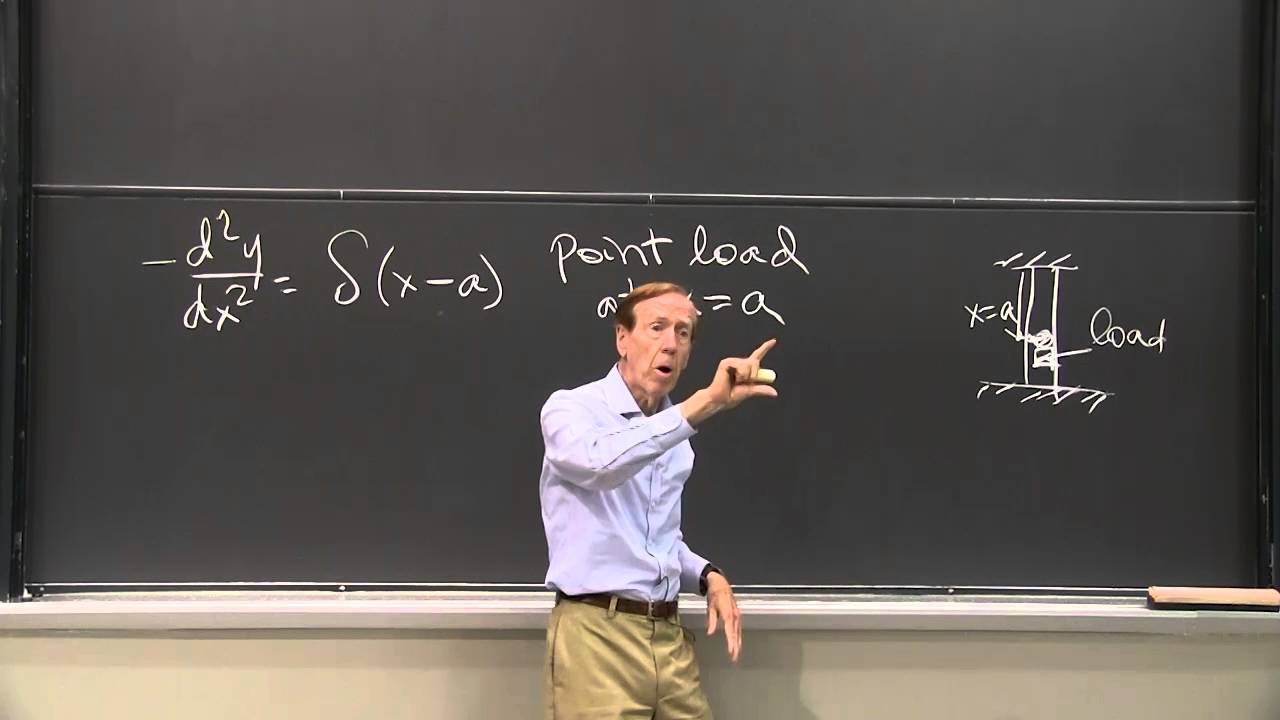
Показать описание
MIT RES.18-009 Learn Differential Equations: Up Close with Gilbert Strang and Cleve Moler, Fall 2015
Instructor: Gilbert Strang
A second order equation can change from two initial conditions to boundary conditions at two points.
License: Creative Commons BY-NC-SA
Instructor: Gilbert Strang
A second order equation can change from two initial conditions to boundary conditions at two points.
License: Creative Commons BY-NC-SA
Boundary Conditions Replace Initial Conditions
Boundary and Initial Conditions
MEGR3116 Chapter 2.4: Boundary and Initial Conditions
Boundary and Initial Value Problems | Lecture 60 | Numerical Methods for Engineers
Differential Equation - 2nd Order (29 of 54) Initial Value Problem vs Boundary Value Problem
HEC-RAS 2D Class: 2.8 - Boundary and Initial Conditions
BOUNDARY AND INITIAL CONDITIONS || PARTIAL DIFFERENTIAL EQUATIONS
Solving the heat equation | DE3
Mass transfer in English | 25 | What are boundary conditions and initial conditions?
Lecture 10 Boundary and initial Condition
Section 2.1 - Boundary Conditions
Boundary Value Problem (Boundary value problems for differential equations)
PDE examples & boundary conditions
Initial condition and boundary condition
Heat Transfer | U2-L6 | Boundary and Initial Conditions - 1
[HT-6] Boundary and Initial Conditions - Heat Diffusion Equation
Fluid Mechanics Lesson 11B: Boundary Conditions for the Navier-Stokes Equation
Heat Equation PDE Neumann boundary condition
Intro to Boundary Value Problems
Oxford Calculus: How to Solve the Heat Equation
Lec 3: Initial and boundary conditions
Boundary and initial/final conditions in the Black-Scholes equation
Three Ways to Solve a Differential Equation With Boundary Conditions
Heat Transfer L4 p3 - Common Boundary Conditions
Комментарии
 0:17:03
0:17:03
 0:07:47
0:07:47
 0:07:07
0:07:07
 0:04:54
0:04:54
 0:02:37
0:02:37
 0:24:33
0:24:33
 0:10:44
0:10:44
 0:14:13
0:14:13
 0:07:30
0:07:30
 0:15:17
0:15:17
 0:05:52
0:05:52
 0:05:02
0:05:02
 0:27:15
0:27:15
 0:01:48
0:01:48
 0:05:33
0:05:33
![[HT-6] Boundary and](https://i.ytimg.com/vi/xpFl-Jk3Gfk/hqdefault.jpg) 0:13:51
0:13:51
 0:13:28
0:13:28
 0:18:51
0:18:51
 0:08:51
0:08:51
 0:35:02
0:35:02
 0:50:54
0:50:54
 0:07:22
0:07:22
 0:37:37
0:37:37
 0:12:06
0:12:06