Ex 7: Find the Zeros of a Degree 5 Polynomial Function

preview_player
Показать описание
This video provides an example of how to find the zeros of a degree 5 polynomial function given one imaginary zero with the help of a graph of the function. The function has 2 imaginary zeros, 2 irrational zeros and 1 rational zero.
  1. Mathispower4u
  2. zeros
  3. roots
  4. find
  5. imaginary
  6. complex
Рекомендации по теме
Ex 7: Find 0:08:43

Ex 7: Find the Zeros of a Degree 5 Polynomial Function

find the zeros 0:04:04

find the zeros of quadratic polynomial x^2+7x+10 And verify the relationship between zeros and coeff

Ex 4: Find 0:05:40

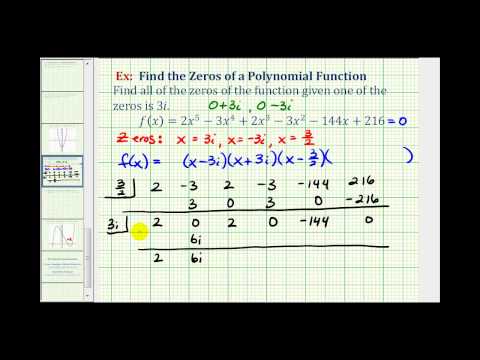
Ex 4: Find the Zeros of a Polynomial Function with Imaginary Zeros

Finding All of 0:05:35

Finding All of the Zeros of a Polynomial Including Complex

Ex 1: Find 0:06:09

Ex 1: Find a Quadratic Function Using Sum and Product of Zeros (Integer and Fraction Zeros)

HSC Maths Ext2 0:05:26

HSC Maths Ext2 - Complex Numbers - Finding Square Roots of Complex Numbers

Ex 3: Find 0:05:55

Ex 3: Find the Zeros of a Polynomial Function with Irrational Zeros

Ex 2: Find 0:05:16

Ex 2: Find the Zeros of a Polynomial Function - Real Rational Zeros

ICSE class 8 0:37:57

ICSE class 8 Super maths star Chapter 4 Cube and cube roots Ex 4.1

Find zeros of 0:05:04

Find zeros of the quadratic polynomial 6x2-3-7x |Find the zeros of 6x2-3-7x|Ex 2.2 Class 10 Maths Q1

6x2-3-7x Find the 0:04:37

6x2-3-7x Find the Zeros of each of the following quadratic polynomials and verify the relationship

Find x | 0:04:14

Find x | Solve Quadratic Equations by Factoring | Find the Zeros of the Polynomial x2+7x+10

x2+7x+12 Find the 0:03:31

x2+7x+12 Find the zeros of the following quadratic polynomials and verify the relationship between

How to Determine 0:03:19

How to Determine the Multiplicity and Zeros of a Polynomial

Ex 2: The 0:07:58

Ex 2: The Zero Feature of the TI84 to Find Rational Zeros of a Polynomial

Ex 1: Find 0:07:54

Ex 1: Find the Zeros of a Polynomial Function - Integer Zeros

Find the quadratic 0:02:37

Find the quadratic equation whose zeros are 7 and -5

How To Solve 0:04:21

How To Solve Absolute Value Equations, Basic Introduction, Algebra

Root 3x2 + 0:05:01

Root 3x2 + 10x + 7 root 3. Find the Zeros of each of the following quadratic polynomials and verify

Square Roots and 0:05:03

Square Roots and Cube Roots | Math with Mr. J

Alpha & Beta 0:00:22

Alpha & Beta Important Formulas Class 10 Polynomials | Sum of Zeros | Product of zeros | #shorts

If α, β 0:00:53

If α, β are the Zeros of Polynomial p(x) = 2x2 - 4x + 5 then find the value of (α - β)^2

Find a quadratic 0:03:28

Find a quadratic polynomial whose zeros are 5 + √7 and 5 - √7

Finding the polynomial 0:07:46

Finding the polynomial with irrational zeros

Комментарии
Автор

Hello, mr Sousa! I have a question.
Without looking at graph to find out one of the roots, we should first perfom a syntetic division of the polynomial by given amaginary number, divide the quotient by the second imaginary zero, get a polynomial of 3d degree and then to try the rational zero theorem to get another factor and 2nd degree polynomial, which at last we can factored by grouping or by any other technic. Am I right, mr Sousa, or are there other ways to find out the rest of zeros algebraically?   And what if we have even higher nonfactorable degree polynomial, how then we can factor the entire polynomial? Thank you very much again for the videos.

architectEvo