filmov
tv
Cardinality part 2: proof & kth minimum value
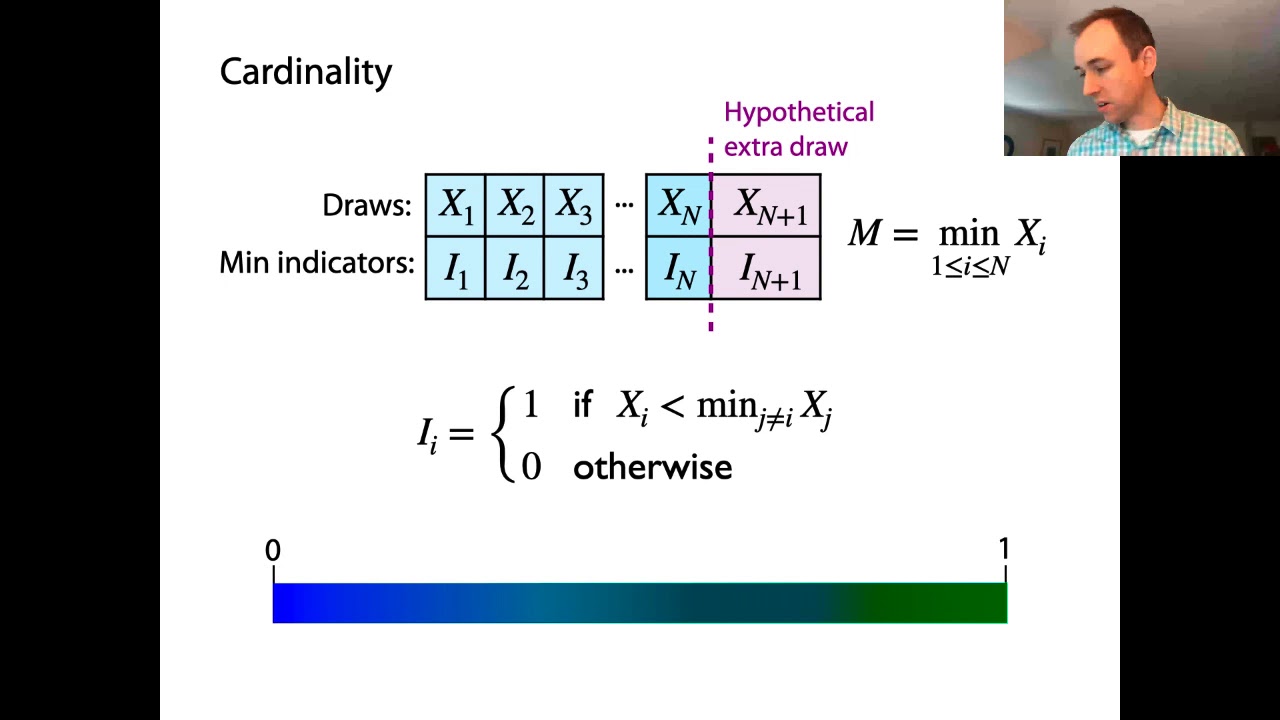
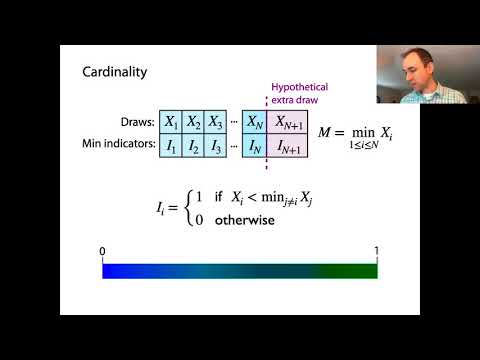
Показать описание
We derive the equation that explains why the "hat-problem" gives an estimate for cardinality. Seeing that we might get a better estimate if we use more than one minimal value, we discuss the "kth minimum value" (KMV) variant and how it uses averaging to obtain a better estimate. Finally, we briefly discuss different ways to use one or more hash functions to get k samples.
These materials are also openly available on figshare. Please cite this work; this ensures that funding agencies see the impact and importance of these open learning materials.
Channel: @BenLangmead
These materials are also openly available on figshare. Please cite this work; this ensures that funding agencies see the impact and importance of these open learning materials.
Channel: @BenLangmead
0:34:44
Cardinality part 2: proof & kth minimum value
0:05:19
Section 5.1, part 2 Examples involving cardinality
0:02:24
Comparing Infinities Part 2: Proving Equal Cardinality Example
0:19:18
Cardinality Part 2
0:11:53
Section 5.1(c), part 2 Cardinality of a finite set
0:19:50
MAT2125 - 2.2 - Cardinality | Part 2 (19:51)
0:03:47
Cardinality condition in Bijection - Part 2
0:05:40
Cardinality of Sets: Proving their equality
0:07:10
Cardinality of the Union, Superquiz 2 Problem 10
0:06:42
Section 5.1(c), part 7 Cardinality of Cartesian product of finite sets
0:02:12
Cardinality condition in Onto function - Part 2
0:03:43
Cardinality condition in One-One function - Part 2
0:06:02
Section 5.1, part 1 Definition that sets have same cardinality
0:08:14
Section 5.1, part 5 A few general results involving cardinality
0:05:04
Cantor's Theorem on the Cardinality of Power Sets
0:20:02
Set Theory Part 2 : Proof using Venn diagram | Cardinality | Principle of Inclusion & Exclusion
0:05:44
Prove the Cardinality of the Integers is the same as the Cardinality of the Even Integers
0:07:15
Section 5.2-5.5, part 10 R2 and R have the same cardinality
0:09:46
Proof: Number of Subsets using Induction | Set Theory
0:11:55
Section 5.1(c), part 3 Cardinality of finite disjoint unions of finite sets
0:25:39
Cardinality -- Proof Writing 22
0:24:41
Math 225 - 4.3 (part 1) Properties of Functions and Cardinality
0:00:18
Symmetric Difference | Complete Concept | Set Theory
0:06:50
Prove the Cardinality of the Integers is the same as the Cardinality of the Odd Integers
Комментарии