filmov
tv
A Non-Standard Radical Equation

Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #RadicalEquations
EXPLORE 😎:
PLAYLISTS 🎵 :
#ChallengingMathProblems #RadicalEquations
EXPLORE 😎:
PLAYLISTS 🎵 :
A Non-Standard Radical Equation
Solving a very radical equation using a non-standard method. An algebraic challenge...
Solving a Non-Standard Radical Equation
Solving a Non-Standard Equation For Reals
Solving a radical equation. Algebra challenge.
LOGARITHMIC/RADICAL EQUATION!!! (Challenging math problem #15)
Solving a very radical equation. An algebraic challenge.
A non-standard quartic equation
WRITING STANDARD EQUATION OF ELLIPSE WITH FOCI AND MINOR AXIS || PRE-CALCULUS
Solving A Non-Standard Equation
Solving an equation in non-standard ways
A radical equation that turns into a quartic
Solving a nonic equation using a non-standard method...An algebra challenge...
Solving Radical Equations with Two Radical Terms • [5.3c] Pre-Calculus 11
A Non-Standard Equation with One Solution (k is positive)
Solving a Non-standard System of Equations | Two Ways
A radical equation solved by using an ingenious method
Traditional Algebra 2 – 8.6 Solving Radical Equations
Solving A Radical Equation Using a Radical Method (maybe)
Solving a Non-standard System of Equations in Two Ways
A Non-Standard Equation with Natural Logarithm
A Non-standard Exponential Equation
A Radical Equation with a Radical Solution
Solving Radical Equations with Different Roots (Example)
Комментарии
 0:09:48
0:09:48
 0:06:54
0:06:54
 0:10:11
0:10:11
 0:04:34
0:04:34
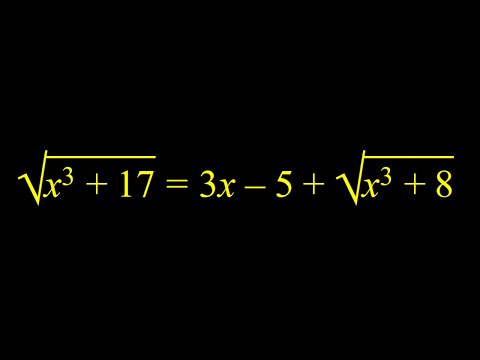 0:10:09
0:10:09
 0:01:04
0:01:04
 0:12:51
0:12:51
 0:06:09
0:06:09
 0:07:04
0:07:04
 0:09:05
0:09:05
 0:16:41
0:16:41
 0:07:30
0:07:30
 0:07:08
0:07:08
 0:10:37
0:10:37
 0:08:42
0:08:42
 0:12:45
0:12:45
 0:07:28
0:07:28
 0:15:54
0:15:54
 0:08:07
0:08:07
 0:12:45
0:12:45
 0:09:56
0:09:56
 0:04:35
0:04:35
 0:05:09
0:05:09
 0:04:16
0:04:16