filmov
tv
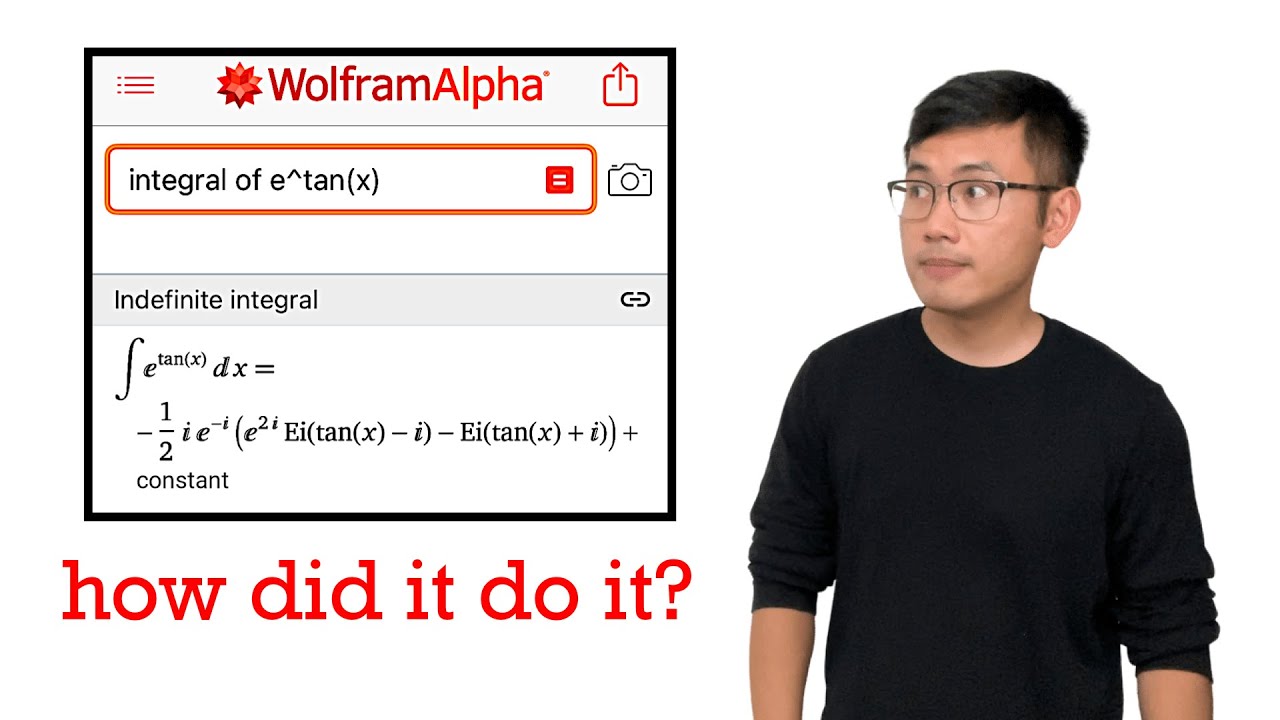
integral of e^tan(x)
Показать описание
How do we do the integral of e^tan(x)? This integral looks very impossible with our typical calculus 2 integration techniques. Here we will need non-elementary functions Ei(x) and li(x). I will show you how to get the answer WolframAlpha gives for the integral of e^tan(x). Note: the result should be real despite how non-real it looks since e^tan(x) is real, to begin with.
@blackpenredpen
@blackpenredpen
integral of e^tan(x)
Evaluate the Integral e^(tan x) sec^2 x dx. Natural exponential function
Integral of e^tan(x)*sec^2(x) - Integral example
How REAL Men Integrate Functions
Integral of e^(tan x)sec^2 x
INTEGRAL of TANGENT tan x, INTEGRALS, #math #maths #exams #university
Integral of tan x dx
Integral of tanx
Every Student Should See This
Integral of tan x
when calculus students use trig identities too early
Integral of e^x(tan x + sec^2 x) || Integration by parts
Integrating Exponential Functions By Substitution - Antiderivatives - Calculus
Integration of tanx // integration by substitution ( calculus )
Integral of tan(x) - Integration by Substitution, Calculus 2
I Computed An Integral That Breaks Math
Integral of e^sqrt(x)
Integrate e^(tan^-1 x)/(1+x^2)
Class 12th – Integral of tan x dx | Integrals | Tutorials Point
When mathematicians get bored (ep1)
It 'Cannot' Be Done (Integrals)
Integral of 1/(1+e^x)
100 integrals (world record?)
Differentiation and integration important formulas||integration formula
Комментарии
 0:07:41
0:07:41
 0:01:49
0:01:49
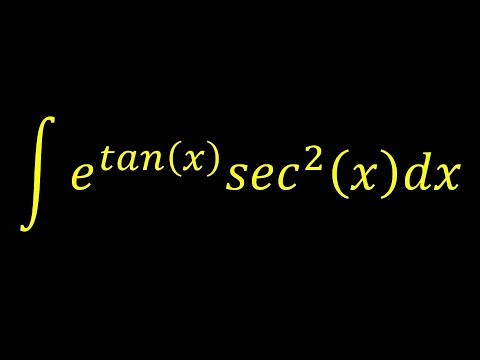 0:02:05
0:02:05
 0:00:35
0:00:35
 0:02:36
0:02:36
 0:01:00
0:01:00
 0:02:44
0:02:44
 0:05:28
0:05:28
 0:00:58
0:00:58
 0:03:58
0:03:58
 0:00:43
0:00:43
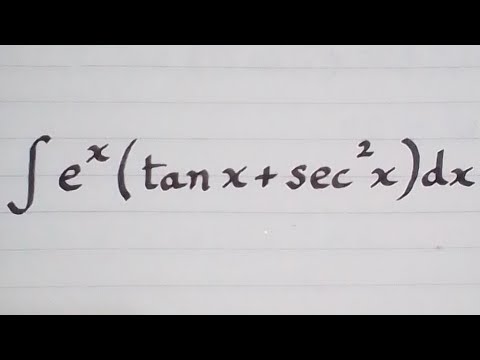 0:03:30
0:03:30
 0:11:16
0:11:16
 0:01:00
0:01:00
 0:02:28
0:02:28
 0:04:20
0:04:20
 0:05:43
0:05:43
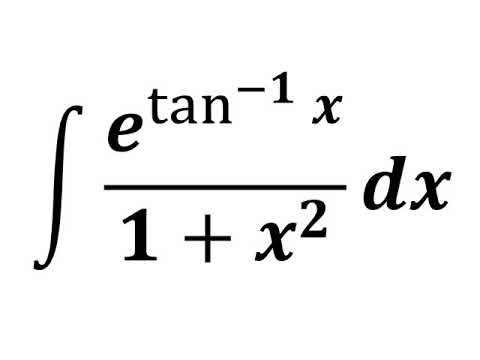 0:02:32
0:02:32
 0:02:39
0:02:39
 0:00:37
0:00:37
 0:03:11
0:03:11
 0:00:58
0:00:58
 5:50:23
5:50:23
 0:00:16
0:00:16