filmov
tv
Proof - Odd composite numbers (3 of 3: By contradiction)

Показать описание
Proof - Odd composite numbers (1 of 3: Setup)
Proof - Odd composite numbers (2 of 3: Understanding the negation)
Proof - Odd composite numbers (3 of 3: By contradiction)
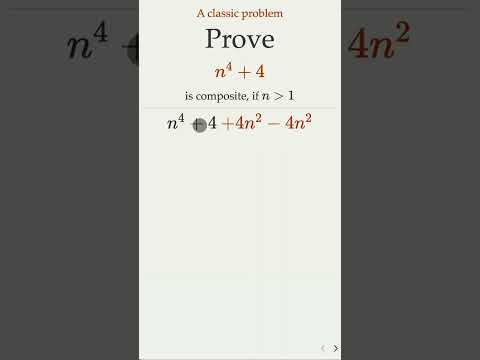
Prove n^4+4 Is Composite
Prime Numbers and Composite Numbers
Odd Times Odd is Odd Proof
Prime Numbers - Magic Trick!! - Part 1 | Fun Math | Don't Memorise
contradiction proof: infinite number of odd numbers
Prime Numbers and the Fundamental Four - Historical Breakthrough
Lec 28 - Proving A Number Is Composite
Factors of All Odd Composite Numbers (1 - 100) _ Principal Sir
Direct Proof: Prove that if 5x - 7 is odd, then 9x + 2 is even
Formal Definitions in Math | Ex: Even & Odd Integers
How to Prove Math Theorems | 1st Ex: Even + Odd = Odd
Proof - Sum & Difference of squares of Odd Prime Numbers is Composite Number
Human Calculator Solves World’s Longest Math Problem #shorts
What are Prime Numbers? | Math with Mr. J
Prime Number or Composite Number?? How to know if the number is prime or not? #fastandeasymaths
If a and b are two odd prime numbers greater than 3, show that a^2 – b^2 is composite
maths prime,even,odd,composit number
Proving 'Prime Gaps' Can Be 'Arbitrarily Large' in 1 Minute! #shorts
Differences between two consecutive square number are odd #Math #YouTube shorts
How to show or prove that multiplying 2 odd numbers together results in an odd number answer
FULL FORM OF MATHS😍#maths #MATHSFUN#shorts #viral
Комментарии
 0:08:56
0:08:56
 0:07:46
0:07:46
 0:10:58
0:10:58
 0:01:00
0:01:00
 0:06:23
0:06:23
 0:05:04
0:05:04
 0:00:39
0:00:39
 0:04:07
0:04:07
 0:14:22
0:14:22
 0:04:26
0:04:26
 0:03:14
0:03:14
 0:03:54
0:03:54
 0:03:23
0:03:23
 0:08:35
0:08:35
 0:03:49
0:03:49
 0:00:34
0:00:34
 0:04:46
0:04:46
 0:10:38
0:10:38
 0:02:40
0:02:40
 0:00:05
0:00:05
 0:00:59
0:00:59
 0:00:15
0:00:15
 0:04:48
0:04:48
 0:00:41
0:00:41