(EViews10) - How to Estimate ARCH Models #arch #timeseries #volatility #modeling #econometrics

This video simplifies the understanding of the autoregressive conditional heteroscedasticity (ARCH) using an approach that beginners can grasp. The video series will contain four other tutorials: (1) How to Simulate ARCH model; (2) How to Test for the presence of ARCH Effects; (3) How to Estimate ARCH Models and (4) How to Forecast ARCH Volatility. So, what is ARCH? Autoregressive indicates that heteroscedasticity observed over different time periods may be autocorrelated; conditional informs that variance is based on past errors; heteroscedasticity implies the series displays unequal variance. Popularised by Nobel Prize Winner, Robert F. Engel (1982)

Why use ARCH: Models the attitude of investors not only towards expected returns but also towards risk (uncertainty); Relates to economic forecasting and measuring volatility; Techniques  ARCH, ARCH-M, GARCH, GARCH-M, TGARCH and EGARCH; Concerned with modeling the volatility of the variance; Conditional and time-varying variance; Deals with stationary (time-invariant mean) and nonstationary (time-varying mean) variables; Nonstationary  varying mean; Heteroscedastic  varying variance; Concerns financial and macroeconomic time series; Duration  daily, weekly, monthly, quarterly (high frequency data); Financial/economic series  stock prices, oil prices, bond prices, inflation rates, exchange rates, interest rates, GDP, unemployment rates etc.

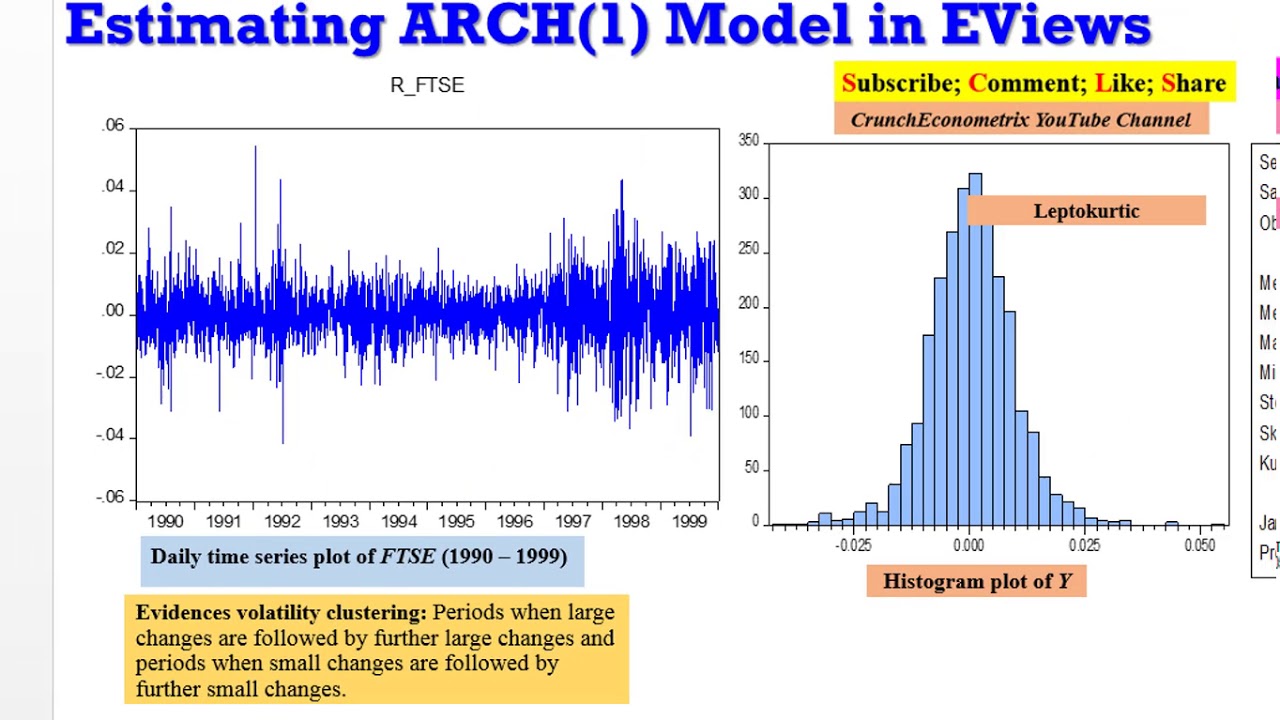
What is conditional variance? The assumption of homoscedasticity (constant variance) is very limiting, hence preferable to examine patterns that allow the variance to depend (conditional) on its history. Volatility: When the values of financial variables change rapidly from time to time in an apparently unpredictable manner. Volatility Clustering: Periods when large changes are followed by further large changes and periods when small changes are followed by further small changes. Shows wild and calm periods.

The ARCH Estimator: The presence of ARCH does not affect consistency of OLS. Still has desirable properties under ARCH. OLS yields consistent but inefficient estimates. Estimates of the covariance matrix will be biased. Leading to invalid t-statistics. Remember, these are valid for any form of heteroskedasticity, and ARCH is just one particular form of heteroskedasticity. An efficient estimator is required  maximum likelihood algorithm.
Some Lessons Learnt: The time-varying variance is modeled by the procedure called autoregressive conditional heteroscedasticity (ARCH); ARCH simply conveys that the series in question has a time-varying variance (heteroscedasticity) that depends on (conditional on) lagged effects (autocorrelation); ARCH model is intuitively appealing because it explains volatility as a function of the errors. These errors are called “shocks” or “news” by financial analysts. They represent the unexpected!; The larger the shocks, the greater the volatility in the series; Since variance is often used to measure volatility, and volatility is a key element in asset pricing theories, ARCH models have become important in empirical finance; Most financial time series like stock prices, exchange rates, oil prices etc. exhibit random walks in their level form, that is, nonstationary (time-varying means); But stationary at 1st difference which often exhibit wide swings or volatility; Wide swings suggest that the variance of the financial time series changes over time (time-varying volatility); Volatility clustering  big changes in u_t are fed into further big changes in h_t via the lagged effects u_(t-1); ARCH modeling has become increasingly popular; useful for modeling volatility; especially changes in volatility over time (that is, time-varying volatility).

References and Readings: Asteriou and Hall (2016) Applied Econometrics, 3ed; Hill, Griffiths and Lim (2008) Principles of Econometrics, 3ed; Roman Kozan (2010) Financial Econometrics with EViews; Gujarati and Damodar (2009) Basic Econometrics, International Edition; R. Engle, “Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation,” Econometrica, vol. 50. No. 1, 1982, pp. 987–1007; A. Bera and M. Higgins, “ARCH Models: Properties, Estimation and Testing,” Journal of Economic Surveys, vol. 7, 1993, pp. 305–366.

Follow up with soft-notes and updates from CrunchEconometrix:

[CrunchEconometrix]

Beloved guest/subscriber, you have discovered my amazing YouTube Channel tailored specifically for you and other beginners and intermediate users. Please do not keep me to yourself (lol). Kindly share my videos and links with your students, colleagues and academic community so that they too can SUBSCRIBE and learn with ease….and for the global community to be aware that applied econometrics can be simplified. My teaching approach is very practical. I adopt a do-as-I-do style. Many thanks to those who have supported me by telling others. Once again, CrunchEconometrix loves to teach, support my Channel with your subscription, likes, feedbacks and sharing my videos with your cohorts. Follow me on Facebook, Twitter and Reddit. Love you all, greatly!!!

[babarahmad]

Saving my Masters degree question by question. GOD BLESS

[adisuabebaw]

I thank You very much for your supportive videos. But i would like to ask you a question. How can we measure the level of Volatility and use it for regression purpose?

[kingsleyohanmo]

please can you explain what you mean by 11 iterations before convergence

[kritikaagarwal]

From the analysis how can we analyse the volatilty.. How volatile is the data.

[waqarkhalid]

I have the real exchange rate data on an yearly basis. Could you please please tell me how to find the exchange rate volatility and its figure??? Any supporting video link? Eviews application etc?

[TheLittleTurtle-tuvy]

could you explain what does it mean of "11 iteration to reach convergence"

[estevaomcs]

Always a great explanation, congratulations! Now, what if the coeficiente B1 is greater than 1, what should i do?

[cssunita]

is it necessary to check serial correlation for building arch model?

[moonsafar]

Thank you very much, could recored another video talking about the treatment with data from A to Z ( how can applying the model to decrease the errors)

[__DeaMelindaSimamora]

Hai ma'am
I wanna ask, if we are estimating models to find the best model, but of all those models, the probability is not significant
Can the model still be used for forecasting?

[poppyblop]

How do we know how many ARCH lag we need? How do we know we only need ARCH(1) and not ARCH(2), or AR(1) only etc...?

[shaydenrobinsonmcse]

If your data does not show any arch effects does that mean you cannot estimate an arch model from it?

[kishanpatel-ucgx]

Hi, can you please explain what you mean by the model is explosive if b1>1. its at 6mins 13 seconds into the video. Thanks

[asmarita]

want to ask, if the arima model is not normally distributed, can we continue to the GARCH model?

[dasundesilva]

What does the mean equation tell us and can you specify what the mean equations formula please?

[mmmmjjjjkk]

thanks a lot. how can we estimate the arch model with more than one variable? is it possible?

[PhuPham-gjls]

I have a question, how can I calculate the returns for a particular index given that I have the closing prices?

[randomYtuberr]

When i click "ok" button at @2.41 is get error saying "ARCH estimation requires a continuous sample". Im currently working on 5 year daily data from today downloaded for indian stock index called Nifty50 from yahoo. I have learnt from another youtube video that presence of break-through point matters.? am i getting error message bcoz of that? can u please guide!