filmov
tv
Math olympiad problem you can solve

Показать описание
Mathematical problem from Moscow math olympiad for the graduate class.
#Puzzle #Math #YuriNeuro
Timecodes:
0:00-Intro
0:51-Math Olympiad Problem
0:56- Parametrization
1:32- Logarithm base rule
2:15- Logarithm base (chain) rule derivation
2:54 -Log base rule application for the parametrization
3:32- Simplifing qubic equation
3:45-(x-a)(x-b)(x-c) factorization formula
3:51- Answer
4:51- New math olympiad puzzle to solve
5:17- Share your ideas and check neuroscience videos
Mathematical puzzle from Moscow school mathematical olympiad (2018 and 2021). To solve this math problem one should recall the knoledge about logarithm base (logarithm chain) rules and polynomial factorization. For instance, one should now how to expand (x-a)(x-b)(x-c). However, one should not memorize neither logarithm base change (logarithm switch) rule, nor
(x-a)(x-b)(x-c) formula and can derive them by applying the definition of logartihmic function and guesses about polynomial factoring.
At the end, another mathematical olympiad question from Russian school math olympiad is given for the further discussion.
If you are interested in this mathematical question, check the other videos in this topic.
Other puzzle videos:
If you are interested in science, you can check my recent videos about novel neuroscience research.
Sources:
#Puzzle #Math #YuriNeuro
Timecodes:
0:00-Intro
0:51-Math Olympiad Problem
0:56- Parametrization
1:32- Logarithm base rule
2:15- Logarithm base (chain) rule derivation
2:54 -Log base rule application for the parametrization
3:32- Simplifing qubic equation
3:45-(x-a)(x-b)(x-c) factorization formula
3:51- Answer
4:51- New math olympiad puzzle to solve
5:17- Share your ideas and check neuroscience videos
Mathematical puzzle from Moscow school mathematical olympiad (2018 and 2021). To solve this math problem one should recall the knoledge about logarithm base (logarithm chain) rules and polynomial factorization. For instance, one should now how to expand (x-a)(x-b)(x-c). However, one should not memorize neither logarithm base change (logarithm switch) rule, nor
(x-a)(x-b)(x-c) formula and can derive them by applying the definition of logartihmic function and guesses about polynomial factoring.
At the end, another mathematical olympiad question from Russian school math olympiad is given for the further discussion.
If you are interested in this mathematical question, check the other videos in this topic.
Other puzzle videos:
If you are interested in science, you can check my recent videos about novel neuroscience research.
Sources:
Комментарии
 0:02:52
0:02:52
 0:13:53
0:13:53
 0:01:00
0:01:00
 0:16:04
0:16:04
 0:01:00
0:01:00
 0:11:56
0:11:56
 0:17:08
0:17:08
 0:14:22
0:14:22
 0:08:31
0:08:31
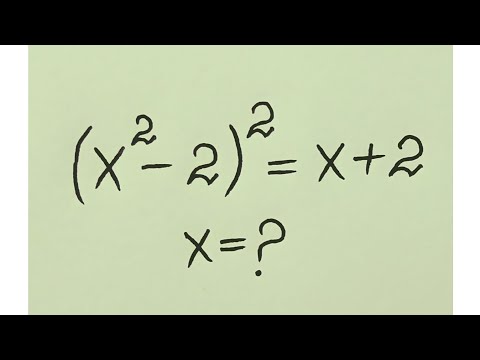 0:10:39
0:10:39
 0:08:36
0:08:36
 0:10:38
0:10:38
 0:10:44
0:10:44
 0:01:54
0:01:54
 0:09:54
0:09:54
 0:10:30
0:10:30
 0:11:15
0:11:15
 0:00:52
0:00:52
 0:11:43
0:11:43
 0:15:15
0:15:15
 0:02:34
0:02:34
 0:02:54
0:02:54
 0:08:18
0:08:18
 0:16:56
0:16:56