filmov
tv
Finding Poles and Zeros using State-space Methods

Показать описание
We show that transfer function poles and zeros can be found by solving eigenvalue problems involving the state-space matrices A, B, C and D.
Finding Poles and Zeros using State-space Methods
Zeros and Poles of a Transfer Function
Finding poles zeros and stability of system
Problem 6: Representation of Poles and Zero in S Plane | Laplace Transform | Signals and Systems
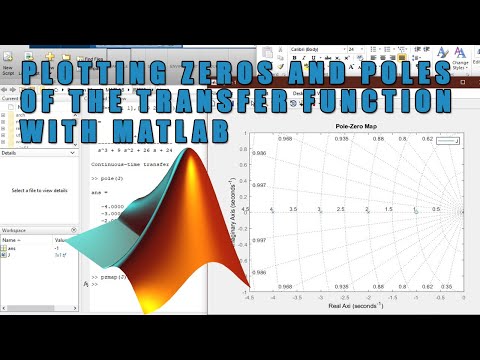
How to find and plot zeros and poles of a transfer function in MATLAB
#19 Finding number of poles and zeros in passive circuits
Finding zeros poles from transfer function in MATLAB
Intro to Control - 7.1 Poles and Zeros
How to find and plot the poles and zeros of transfer functions using matlab.
Finding poles and zeros of a given transfer function in Matlab
How to find poles,zeros and gain from transfer function??? MATLAB
Bode Plots by Hand: Poles and Zeros at the Origin
Finding poles and zeros of a transfer function in Matlab | Urdu
How do Poles and Zeros affect the Laplace Transform and the Fourier Transform?
Plotting of Poles & Zeros of the given Network Function | Network Analysis.
Realizing Poles and Zeros Intuitively || Part -1 || Prep With Me
Finding Poles and Zeros and Other Polynomial Operations in MATLAB - How To Ep. 29
Pole & Zero to Time Domain Response
Location of Poles on the S Plane | Effect on the stability of a System
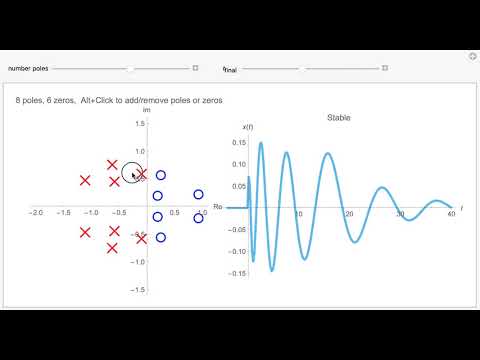
How to plot a pole zero diagram and verify stability
Razavi Electronics2 Lec18: Useful Frequency Response Concepts, Finding Poles by Inspection
Poles & Zeros in a Transfer Function
What are Transfer Functions? | Control Systems in Practice
How to find transfer function from zeros and poles in MATLAB| zp2tf command
Комментарии
 0:14:19
0:14:19
 0:06:39
0:06:39
 0:02:07
0:02:07
 0:08:18
0:08:18
 0:02:54
0:02:54
 0:16:23
0:16:23
 0:02:22
0:02:22
 0:06:30
0:06:30
 0:09:18
0:09:18
 0:03:42
0:03:42
 0:05:44
0:05:44
 0:08:59
0:08:59
 0:02:48
0:02:48
 0:09:16
0:09:16
 0:04:39
0:04:39
 0:31:43
0:31:43
 0:05:08
0:05:08
 0:01:05
0:01:05
 0:04:53
0:04:53
 0:03:19
0:03:19
 0:47:19
0:47:19
 0:05:16
0:05:16
 0:10:07
0:10:07
 0:02:52
0:02:52