filmov
tv
Simplifying a Radical Expression in Three Ways
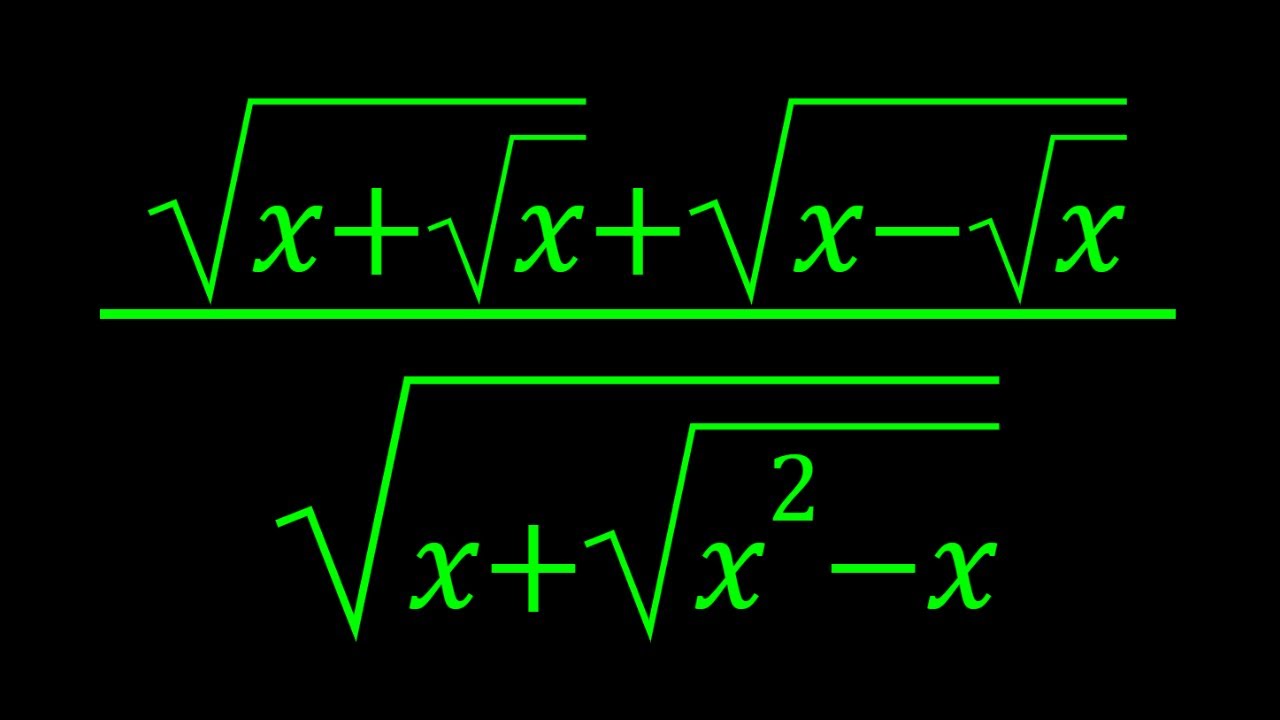
Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #RadicalExpressions
PLAYLISTS 🎵 :
#ChallengingMathProblems #RadicalExpressions
PLAYLISTS 🎵 :
Simplifying Radicals Easy Method
How To Simplify Radicals
Simplify a radical expression with variables
Simplifying Radical Expressions 1
Learn to add and subtract radical expressions
Pre-Algebra 31 - Simplifying Radical Expressions
How to Simplify Radicals (NancyPi)
Simplifying Radicals with Variables and Exponents
Let's Simplify A Radical Expression
Simplifying radical expressions and then combining them
Learn how to simplify a radical
Simplifying a radical expression using rational exponents
Simplifying Radical Expressions - Laws of Radicals
Adding and Subtracting Radical Expressions With Square Roots and Cube Roots
Learn how to simplify a radical expression with variables and a number
Adding and simplifying radicals | Pre-Algebra | Khan Academy
Simplifying a radical expression with the index
Simplifying Radicals
Simplifying the cube root of a radical expression
08 - Rules to Multiply & Divide Radicals in Algebra (Simplifying Radical Expressions)
Simplifying radicals simplify a 4th root radical expression
How To Simplify Square Roots
Algebra 1 - Simplifying Radical Expressions
Simplify Radical Expressions (Quadratic Equation Form)
Комментарии
 0:03:42
0:03:42
 0:13:14
0:13:14
 0:05:14
0:05:14
 0:03:25
0:03:25
 0:03:41
0:03:41
 0:09:28
0:09:28
 0:17:51
0:17:51
 0:03:23
0:03:23
 0:08:37
0:08:37
 0:03:08
0:03:08
 0:04:09
0:04:09
 0:04:26
0:04:26
 0:14:46
0:14:46
 0:11:20
0:11:20
 0:02:42
0:02:42
 0:07:57
0:07:57
 0:02:08
0:02:08
 0:17:58
0:17:58
 0:02:13
0:02:13
 0:29:10
0:29:10
 0:01:53
0:01:53
 0:10:46
0:10:46
 0:15:37
0:15:37
 0:06:10
0:06:10