filmov
tv
Proving logical equivalence involving the biconditional
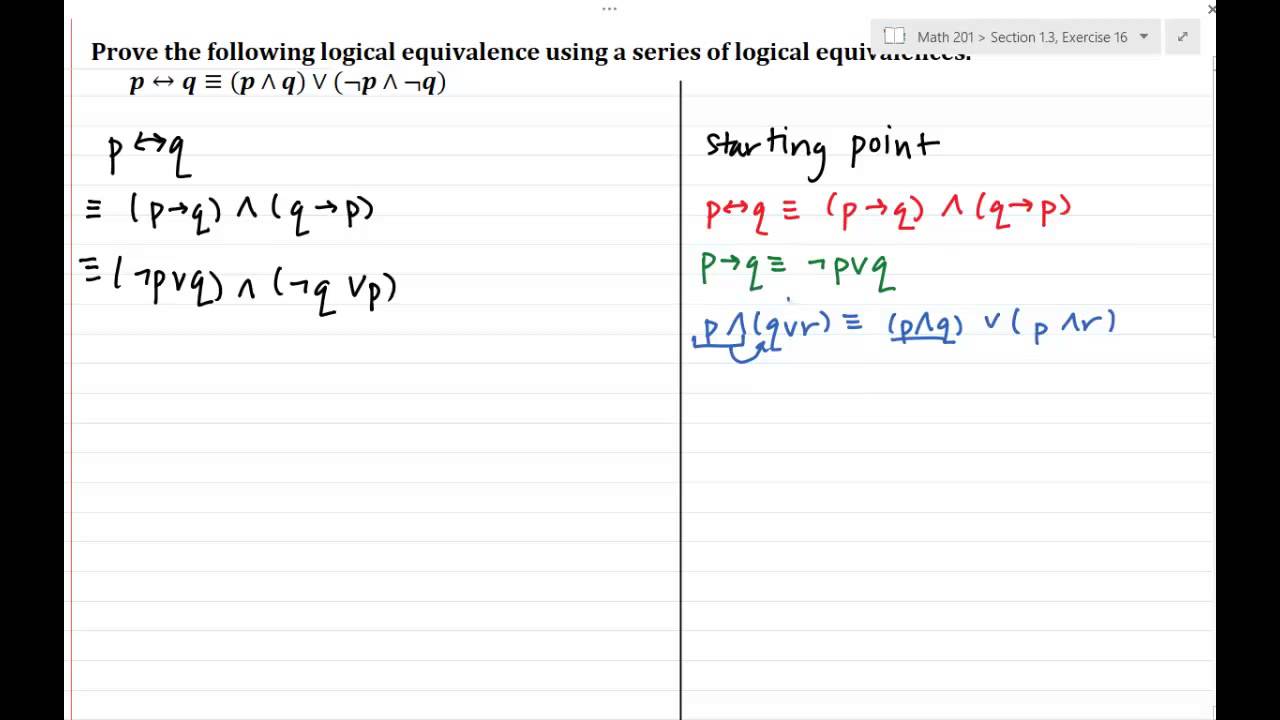
Показать описание
Step by step description of exercise 16 from our text.
Using key logical equivlances we will show p iff q is logically equivalent to (p AND q) OR (NOT p AND NOT q)
Using key logical equivlances we will show p iff q is logically equivalent to (p AND q) OR (NOT p AND NOT q)
Proving a Tautology by Using Logical Equivalences
Propositional Logic − Logical Equivalences
Proving logical equivalence involving the biconditional
7 - (Examples 6-7) Proving Logical Equivalence Using Laws
Logical Equivalence of Two Statements
Logical Equivalence Proof
Prove Logical Equivalence Using Laws
Logical Equivalences Involving Predicates & Quantifiers (Part 1)
sur la philosophie / livre audio français
Proving and Simplifying Propositions using Logical Equivalence Laws
help with week 2 annotating proof with key logical equivalences
Logical Equivalence with out using truth table examples or equivalent formulas examples
Proving logical equivalence 1
Logical Equivalences Involving Predicates & Quantifiers (Part 2)
set up for proving logical equivalence
Logical Equivalence by Truth Tables - Logic - Discrete Mathematics
3 Ways to Show a Logical Equivalence | Ex: DeMorgan's Laws
12 - Logical Equivalence Using Biconditional Statements
Logical equivalence without truth tables (Screencast 2.2.4)
Prove Logical Equivalence Using Laws
Discrete Math - 1.3.1 “Proving” Logical Equivalences with Truth Tables
9 - (Example 9-11) Proving Logical Equivalence Using Laws
17. Tautology by logical equivalences || Tautology without truth table || Discrete Mathematics
Logical Equivalence
Комментарии
 0:06:24
0:06:24
 0:17:23
0:17:23
 0:21:03
0:21:03
 0:05:59
0:05:59
 0:03:42
0:03:42
 0:13:12
0:13:12
 0:05:18
0:05:18
 0:09:12
0:09:12
 8:44:25
8:44:25
 0:07:37
0:07:37
 0:11:57
0:11:57
 0:16:23
0:16:23
 0:07:16
0:07:16
 0:08:48
0:08:48
 0:07:42
0:07:42
 0:09:58
0:09:58
 0:05:29
0:05:29
 0:03:54
0:03:54
 0:07:08
0:07:08
 0:04:38
0:04:38
 0:16:12
0:16:12
 0:09:11
0:09:11
 0:14:24
0:14:24
 0:01:01
0:01:01