Understanding the drivel of 'rates of change' in mainstream calculus.

We usually refer to a rate when we compare two quantities. In ANY mathematical model, it makes NO sense at all to talk about how fast or slow a tangent line changes because no tangent line ever changes. It has been the same in past perpetuity and shall continue to be the same.

In spacecraft, engineering and technology in general, when a rate involves speed, it is usually calculated as a difference quotient with analog input, unless there is a function or model available in which case we refer to a rate at a given time or point, NOT an "instantaneous rate" or "a rate of change".

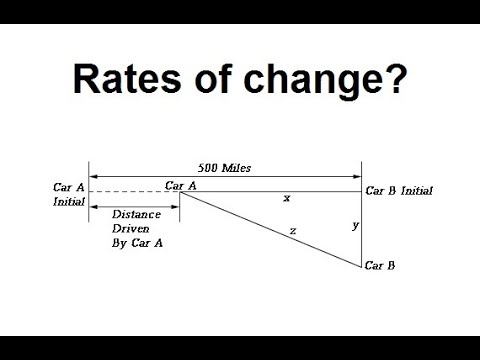
For the example in the video, the question as asked is gibberish, because distance does not change on its own. We talk about how an object moving covers a given distance, but to say the distance changes at a rate means it is being compared to something else, but what?! There is no difference quotient at a given time, only a tangent line slope.

What is time?

Applet used in this video:

There is no such thing as "instantaneous rate":

Paul's Online Notes: