filmov
tv
Trigonometric Substitution: Sin Substitution Example 1| (Ali BA)
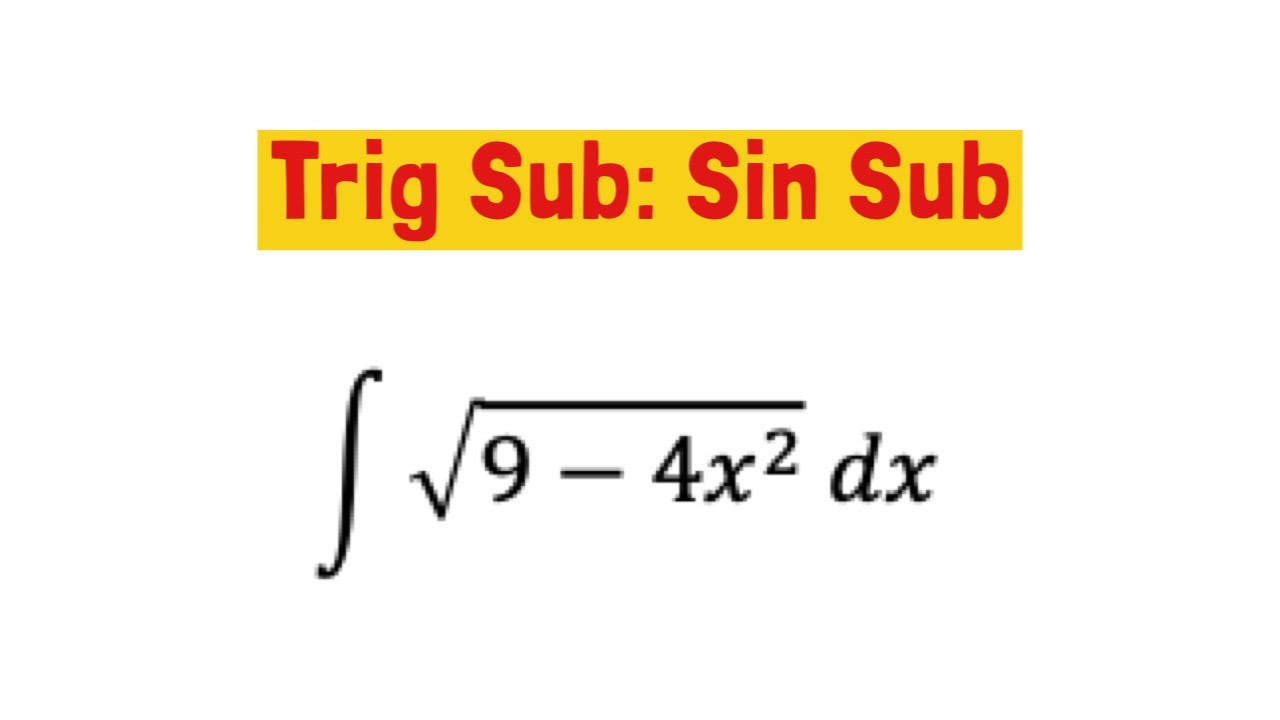
Показать описание
You may wonder how did they construct the table of the integration. One of the answers is that they use trig substitution.
Trig substitution has two types:
1) sin substitution x=a*sin(theta). In case of the integrand has the form: sqrt(a^2-x^2)
To simplify the integrand, we use the trig identity: cos^2+sin^2=1
2)tan substitution x=a*tan(theta). In case of the integrand has the from: a^2+x^2 or square root of that.
To simplify the integrand, we use tan=sin/cos and then we use the trig identity: cos^2+sin^2=1
Note: in some cases, we may need to complete the square of the dominator before we use the trig substitution.
Steps to solve integrals using trig substitution:
1- You make sure that the integrand is in the form of sqrt(a^2-x^2), a^2+x^2 or square root of that.
2- You make the substitution. What is x and dx.
sin substitution x=a*sin(theta). In case of the integrand has the form sqrt(a^2-x^2)
tan substitution x=a*tan(theta). In case of the integrand has the from a^2+x^2 or square root of that
3- You take the integrand and use the trig substitution to re-write it. Then, simplify.
4- You take the integral and use the trig substitution to re-write it. Then, simplify.
5- After you find the antiderivative of step 4, you back substitute the function of theta from step 2.
Remember:
1)arctan(x)=tan^-1(x), arcsin(x)=sin^-1(x)
2)arctan(tan(x))=x, arcsin(sin(x))=x
Table of integration:
If you have any questions or suggestions, let me know in the comments below.
Material in this video is taken from Calculus: Single Variable, 6th Edition by (Hallet, McCallum, Gleason, et al.)
Trig substitution has two types:
1) sin substitution x=a*sin(theta). In case of the integrand has the form: sqrt(a^2-x^2)
To simplify the integrand, we use the trig identity: cos^2+sin^2=1
2)tan substitution x=a*tan(theta). In case of the integrand has the from: a^2+x^2 or square root of that.
To simplify the integrand, we use tan=sin/cos and then we use the trig identity: cos^2+sin^2=1
Note: in some cases, we may need to complete the square of the dominator before we use the trig substitution.
Steps to solve integrals using trig substitution:
1- You make sure that the integrand is in the form of sqrt(a^2-x^2), a^2+x^2 or square root of that.
2- You make the substitution. What is x and dx.
sin substitution x=a*sin(theta). In case of the integrand has the form sqrt(a^2-x^2)
tan substitution x=a*tan(theta). In case of the integrand has the from a^2+x^2 or square root of that
3- You take the integrand and use the trig substitution to re-write it. Then, simplify.
4- You take the integral and use the trig substitution to re-write it. Then, simplify.
5- After you find the antiderivative of step 4, you back substitute the function of theta from step 2.
Remember:
1)arctan(x)=tan^-1(x), arcsin(x)=sin^-1(x)
2)arctan(tan(x))=x, arcsin(sin(x))=x
Table of integration:
If you have any questions or suggestions, let me know in the comments below.
Material in this video is taken from Calculus: Single Variable, 6th Edition by (Hallet, McCallum, Gleason, et al.)
 0:19:50
0:19:50
 0:07:10
0:07:10
 0:15:55
0:15:55
 0:00:39
0:00:39
 0:04:50
0:04:50
 0:24:04
0:24:04
 0:00:43
0:00:43
 0:06:54
0:06:54
 0:51:34
0:51:34
 0:09:04
0:09:04
 0:14:09
0:14:09
 0:08:52
0:08:52
 0:07:31
0:07:31
 0:27:43
0:27:43
 2:09:24
2:09:24
 0:07:42
0:07:42
 0:00:58
0:00:58
 0:19:01
0:19:01
 0:10:37
0:10:37
 0:13:13
0:13:13
 0:22:09
0:22:09
 1:01:49
1:01:49
 0:10:05
0:10:05
 0:09:06
0:09:06