filmov
tv
Lambda Calculus!
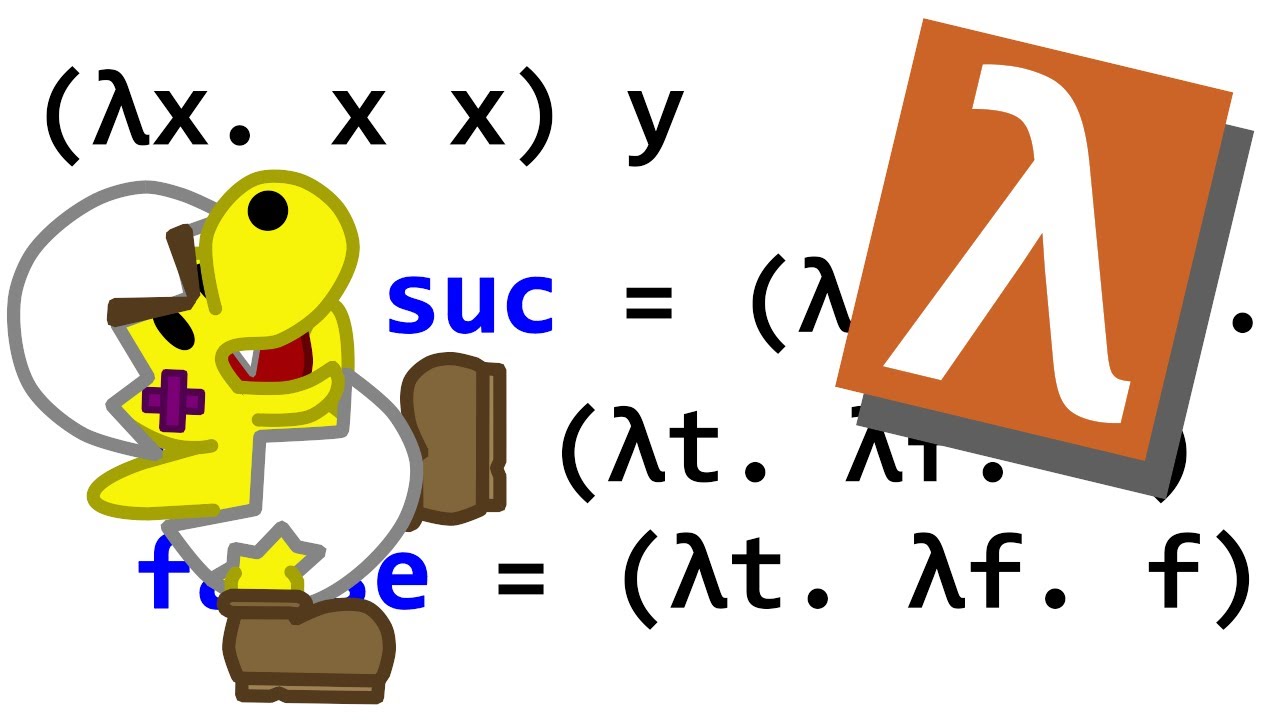
Показать описание
(It's now called the Bale of Esoturtles because why not.)
Have you ever wanted to have a programming language/mathematical system that literally just took functions and applied other functions to them? Well too bad, because that's what Lambda Calculus is! And it's Turing complete, so shut up about it being limited.
LINKS:
MUSIC:
"Jr Troopa Theme" from Paper Mario 64
"Bit Shift" by Kevin MacLeod
"Monody" by TheFatRat
"The Last Dungeon - Encore" from Wonder Boy: The Dragon's Trap
Have you ever wanted to have a programming language/mathematical system that literally just took functions and applied other functions to them? Well too bad, because that's what Lambda Calculus is! And it's Turing complete, so shut up about it being limited.
LINKS:
MUSIC:
"Jr Troopa Theme" from Paper Mario 64
"Bit Shift" by Kevin MacLeod
"Monody" by TheFatRat
"The Last Dungeon - Encore" from Wonder Boy: The Dragon's Trap
Programming with Math | The Lambda Calculus
Lambda Calculus - Computerphile
Lambda Calculus!
Lambda Calculus - Fundamentals of Lambda Calculus & Functional Programming in JavaScript
Learn Lambda Calculus: The language with ONLY FUNCTIONS
Lambda Calculus For Dummies: What is a lambda expression
Why functions are turing complete (Lambda Calculus)
Haskell in 100 Seconds
proglangcast ep 14: Bye Bye Again BQN
Lambda (λ) Calculus Primer
What is Lambda Calculus and why?
Lambda calculus in 5 minutes
Lambda Calculus For Dummies: Introduction
Lambda Calculus: The foundation of functional programming, and the simplest programming language
Seven times Eight in Lambda Calculus
Essentials: Functional Programming's Y Combinator - Computerphile
How to loop in a loopless language (Y Combinator)
What is Lambda Calculus? (ft. Church Encodings)
Lambda (λ) calculus evaluation rules (δ, β, α, η conversion/reduction)
L16: Lambda Calculus Introduction
Semantics: Lambda Calculus and Types
How Can One Greek Letter Help Us Understand Language? Lambda Calculus
Lambda Calculus & Scheme
Lambda Calculus vs. Turing Machines (Theory of Computation)
Комментарии
 0:21:48
0:21:48
 0:12:40
0:12:40
 0:09:51
0:09:51
 1:02:15
1:02:15
 0:12:48
0:12:48
 0:06:09
0:06:09
 0:03:59
0:03:59
 0:02:30
0:02:30
 1:00:01
1:00:01
 0:34:26
0:34:26
 0:08:52
0:08:52
 0:04:33
0:04:33
 0:04:32
0:04:32
 0:15:43
0:15:43
 0:00:07
0:00:07
 0:13:26
0:13:26
 0:03:05
0:03:05
 0:15:11
0:15:11
 0:16:55
0:16:55
 0:15:35
0:15:35
 0:19:08
0:19:08
 0:11:21
0:11:21
 0:15:02
0:15:02
 1:08:24
1:08:24