filmov
tv
Trigonometry - Working with linear and angular speed

Показать описание
Trigonometry - Working with linear and angular speed
And You Thought Trigonometry Was Pointless…
Trigonometry For Beginners!
GCSE Maths - What on Earth is y = mx + c #67
Radians and Degrees
Solving Trigonometric Equations - How to Write General Solution
Old Trigonometry Book #mathematics
2023 GCE Trigonometry | sine rule | Area | Shortest Distance.
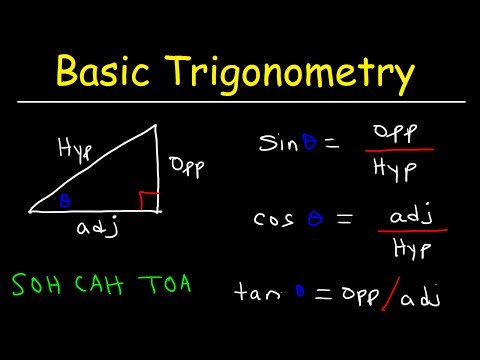
Basic Trigonometry | A-Level Mathematics 9709
Using Algebra and Geometry in the Real World
Function | Linear programming | Trigonometry | Algebra Exam questions and solutions.
The Math behind (most) 3D games - Perspective Projection
Super Rare Algebra & Trigonometry Book
Trigonometry Video 3.4.1 Linear Speed vs Angular Speed
Matrix & Trigonometry (Worked Example)
Interesting Trigonometry Problem | cos(sinx)=1/2
Amazing Book for Learning Trigonometry
The Hardest Math Test
Solving Trigonometric Equations By Finding All Solutions
Linear Speed and Angular Velocity
Trigonometry formula chart |important formula |Trigonometry |shorts
Algebra and Trigonometry Book
😍😍😍 #shorts #mathematics #math #mathvideos #satmath #sat #trigonometry
Essential Mathematics For Aspiring Game Developers
Комментарии
 0:08:33
0:08:33
 0:01:00
0:01:00
 0:21:52
0:21:52
 0:04:53
0:04:53
 0:18:55
0:18:55
 0:06:26
0:06:26
 0:00:42
0:00:42
 0:12:06
0:12:06
 0:34:12
0:34:12
 0:02:41
0:02:41
 0:21:47
0:21:47
 0:13:20
0:13:20
 0:00:47
0:00:47
 0:06:00
0:06:00
 0:04:26
0:04:26
 0:00:49
0:00:49
 0:00:54
0:00:54
 0:00:28
0:00:28
 0:11:49
0:11:49
 0:18:58
0:18:58
 0:00:16
0:00:16
 0:00:56
0:00:56
 0:00:13
0:00:13
 0:47:06
0:47:06