filmov
tv
Integrating the fractional part of a logarithm function
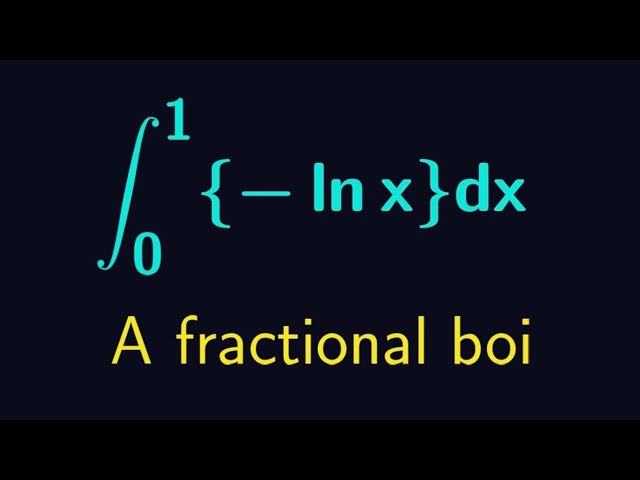
Показать описание
My first fractional part integral and the solution development is pretty elegant indeed.
Integral of fractional part of x from 0 to 4
Integration By Partial Fractions
integrating the FRACTIONAL PART function?!
Integrating the fractional part of a logarithm function
Integration of fractional part function | Integration shortcut #shorts
integration shortcut trick 🔥 for fractional part function
Integration of Fractional Part Function #SHORTS #MATHS
Only 1% Students can Solve This | Integration of Fractional Part by GP Sir
What’s Next?: US Relations in the Age of Trump? Panel 2 – The Border
when an equation has the floor and the fractional part functions
Fractional Part Integrals are COOL!
Definite integral of fractional part function Part
Integral of fractional part of x from 0 to 4
Integral of Fractional Part
Integration of greatest integer and fractional part of functions | JEE main 2019 | mathematicaATD
An interesting integral with fractional part and floor function
#integration of fractional part function #shortcut #trickymaths #integraltricks
Partial Fraction Decomposion
Solving Another Challenging Integral Including the Fractional Part and Floor Functions!
Integration trick |Integration of fractional part function
Fractional part of function. #function #maths #jeemains #jeeadvance #jugalsir
Floor, Ceiling, Fractional part all in one integral problem
What Integration Technique Should I Use? (trig sub, u sub, DI method, partial fractions) calculus 2
Integration of Rational Function by Partial Fractions part 1
Комментарии
 0:07:36
0:07:36
 0:41:07
0:41:07
 0:11:12
0:11:12
 0:09:51
0:09:51
 0:00:22
0:00:22
 0:00:31
0:00:31
 0:00:42
0:00:42
 0:04:39
0:04:39
 1:16:08
1:16:08
 0:05:55
0:05:55
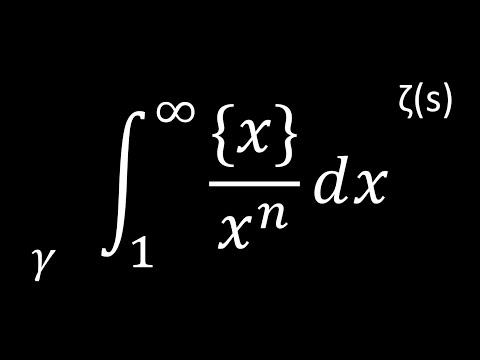 0:15:53
0:15:53
 0:12:01
0:12:01
 0:00:47
0:00:47
 0:19:55
0:19:55
 0:08:36
0:08:36
 0:08:02
0:08:02
 0:00:10
0:00:10
 0:14:12
0:14:12
 0:06:09
0:06:09
 0:00:33
0:00:33
 0:00:57
0:00:57
 0:08:24
0:08:24
 0:22:40
0:22:40
 0:08:11
0:08:11