Base 60 (sexagesimal) - Numberphile

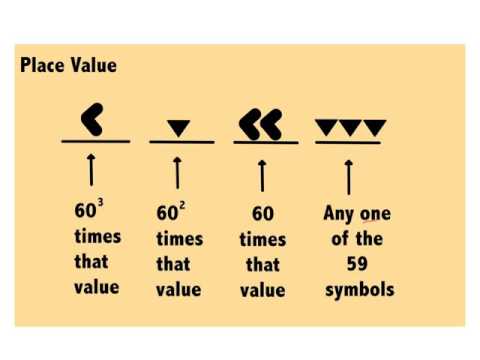
The ancient Babylonians used a number system with base 60 (sexagesimal).
More links & stuff in full description below ↓↓↓

NUMBERPHILE

Videos by Brady Haran

[georgemissailidis]

"So the number we are talking about is 60....it is quite a big number.... ...." And the previous video I watched was about TREE(3)

[CadaverSplatter]

The Babylonians followed the Sumerians in this. The system alternated between 10 and 60 depending on the numeric place. So for the single digits you went 1-10, but for their 10's place, they went up to 60. In their "hundreds place" they would use up to 10 units of sixty, and, the pattern continued in alternating between 10's and 6's in that way.

[raydredX]

I'd love to see many numerical representation systems from various languages.
Not sure they're very knowledgeable about them. I love languages, I love linguistics, I love math. That's why I know a bit about it. Many people in Math don't like languages that much. But maybe! It'd be awesome! Hopefully numberphile's reading this.

[anabulatovic]

"you can cook half of a meal" 😂😂😂😂

[phodd]

They wrote numbers the same way we write time, so each of the base-sixty 'digits' is written in base-ten, but carries to the left occur after that. There's an example in the video on the Babylonian tablet: The sequence 1 24 51 10 is actually a base-sixty fraction that we'd write 1.24:51:10 if we followed time-style formatting and translates as approximately 1.414213 decimal. It's the square root of two... which is the length of the diagonal of the square it's written against!

[macronencer]

I was hoping you might mention the fact that the Babylonians had a floating point system (which I find amazingly interesting!).

[yogiiification]

A more in depth video about the Babylonians and their counting/numeracy system from Brady would be fantastic!

[kofi-tawiahagyeman]

Great videos! The sexagesimal system wasn't devised by the Babylonians. It was actually created by the Sumerians of Sumer Civilization in the 4th millennium BC, many many centuries before adoption by the Babylonians.

[numberphile]

Like the number 60 - why not check out the sixtysymbols channel by the same film-maker as numberphile!? :)

[jonyeahyeahhhhh]

This was superbly clear, when you said they used their knuckles, I immediately counted to 15 by including my thumb, so I had the 30 x 2 for 60 but your method worked also which I think highlights the power of using base 60.

[prettyigirl]

The symbol he drew for 57 is a unique symbol for 57. If he drew another number next to it (say 25) the resulting number would be equal to : 57 * 60 + 25 = 3445
This is the same as our base ten: 36 = 3 * 10 + 6

[ThePeaceableKingdom]

I have read speculation (perhaps this is "out-of-date" and no longer a current speculation among experts...) that the Babylonian system arrived at base 60 as a way to integrate various multiple earlier counting systems across its territory, as 60 could reconcile various systems based on 5 (hand), 10 (fingers), 12 (knuckles), etc...

[barkspawn]

Doesn't this mean they used base 10? If the ones column counts up to 9 then 'rolls over' and they put the 10 in the next column... that's the definition of base 10 isn't it??

[badhombre]

The Babylonian counting system evolved around an economy based on poppy. Ten plants are efficiently stacked 1, 2, 3, 4 in a 60 degree arc segment, of which 6 completes a circular plot. This is reflected in the symbols; for the digits 1-9 plants and then 10 is folded into the arc segment. These plots can then be efficiently stacked with hexagonal packing, where each is surrounded by 6 others.
So, from planting, harvesting and trading, they could very efficiently count their product.

[eurovisioncyan]

2520 is divisible by 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.

[raydredX]

That's how we usually represent bases but there can be more "artistic" ways to represent numbers.
The Babylonians apparently used a mix of 60 and 10 based system.
There's also Romans for example which use a mess of symbols with base ten. III=3 IV=4 V=5 VI=6 for example.

[TimeSplitt]

Thought the link between 60, calendar, length of day a bit confusing/lacking. But that's to be expected with a quick interview, and the video is much appreciated.

But it seems it's such a huge missed opportunity! To teach about the origin of our time & calendar system!

I understand that's a lot of work though (getting the right animations, narration, etc), and again, the video's much appreciated anywho! And if anything it makes you go and research it - hopefully finding a well organised youtube video that pedagogically well organised, explaining the origin of time & calendar.

[leightonjulye]

The seven-day week being approximately a quarter of a lunation has been proposed (e.g. by Friedrich Delitzsch) as the implicit, astronomical origin of the seven-day week. Problems with the proposal include lack of synchronization, variation in individual lunar phase lengths, and incompatibility with the duodecimal (base-12) and sexagesimal (base-60) numeral systems, historically the primary bases of other chronological and calendar units

[audreyteachesmath]

out of curiosity, of the babylonians were so heavily reliant on the number 12 when finger counting, why do we think they flipped their stylus to make the different mark for 10 instead of flipping it for 12?

[AIimageGirl]

You're referring to the mathematical framework that enables us to formulate and analyze theoretical concepts! There are several mathematical systems and tools used to develop and explore theoretical ideas, depending on the context and field of study. Here are a few examples:

1. Mathematical Logic: A formal system used to express and analyze mathematical statements, arguments, and proofs.
2. Category Theory: A branch of mathematics that studies the commonalities and patterns between different mathematical structures, providing a framework for abstracting and generalizing concepts.
3. Type Theory: A system for expressing and analyzing mathematical concepts using types, which can be seen as a formalization of mathematical structures and relationships.
4. Model Theory: A branch of mathematical logic that studies the relationship between formal theories and their models, enabling us to reason about theoretical concepts.
5. Differential Geometry: A mathematical framework for describing and analyzing geometric objects and their properties, crucial for theories like General Relativity.
6. Operator Algebras: A mathematical framework for studying linear operators and their algebras, essential for Quantum Mechanics and Quantum Field Theory.
7. Homological Algebra: A branch of abstract algebra that studies the properties of algebraic structures using homology and cohomology theories.

Some specific mathematical systems used to develop and analyze theoretical concepts include:

1. Hilbert's Formalism: A formal system for mathematics, which provides a foundation for mathematical logic and proof theory.
2. Zermelo-Fraenkel Set Theory: A formal system for set theory, which provides a foundation for modern mathematics.
3. Non-standard Analysis: A mathematical framework for working with infinitesimal and infinite numbers, developed by Abraham Robinson.
4. Causal Dynamical Triangulation: A quantum gravity theory that uses a discretized spacetime, similar to lattice gauge theory.

These mathematical systems and tools enable us to develop, analyze, and refine theoretical concepts, making them essential for advancing our understanding of the world.