filmov
tv
ODE existence and uniqueness theorem

Показать описание
In this video, I prove the famous Picard-Lindelöf theorem, which states that, if f is Lipschitz, then the ODE y’ = f(y) with a given initial condition always has a unique solution (at least in the local sense). The proof involves some neat analysis; more precisely we use the Banach fixed point theorem, featured in another video of mine. Finally, I’ll give some examples of non uniqueness and nonexistence when the assumptions aren’t satisfied. Enjoy!
The Big Theorem of Differential Equations: Existence & Uniqueness
ODE | Existence and uniqueness idea
Existence & Uniqueness Theorem, Ex1
Existence and Uniqueness of Solutions (Differential Equations 11)
Existence and Uniqueness
Differential Equations - Existence and Uniqueness Theorem
ODE existence and uniqueness theorem
The Theory of 2nd Order ODEs // Existence & Uniqueness, Superposition, & Linear Independence
ODE | Existence and uniqueness example
Existence and Uniqueness Theorem Examples
Existence and Uniqueness
Existence & Uniqueness Theorem, Ex3
Existence and Uniqueness Theorem for First Order O.D.E. (Part-1)
Existence and Uniqueness Theorem for First Order Linear Differential Equations
Existence and Uniqueness theorem and how to use it in an example
Existence and Uniqueness - Dynamical Systems | Lecture 4
Existence and Uniqueness Theorems for Ordinary Differential Equations, Introduction to Phase Lines
Mod-04 Lec-18 Picard's Existence and Uniqueness Theorem
(ODE21) Proving The Existence And Uniqueness Theorem (Part 1/3) - Solutions As Fixed Points
ODE Lecture-10: Picard's Theorem (Existence & Uniqueness Theorem) Explained in easy Way || ...
Existence and Uniqueness Theorem
Existence & Uniqueness of Solutions | Numericals | Higher Order Differential Equations | Maths
Existence and Uniqueness Theorem for Higher-Order Linear DE
Existence and Uniqueness theorem and actual solutions of separable first order
Комментарии
 0:12:22
0:12:22
 0:03:52
0:03:52
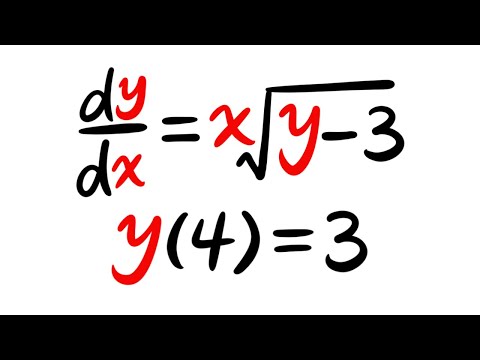 0:11:22
0:11:22
 0:44:32
0:44:32
 0:06:23
0:06:23
 0:07:23
0:07:23
 0:40:36
0:40:36
 0:11:19
0:11:19
 0:04:44
0:04:44
 0:17:11
0:17:11
 0:08:16
0:08:16
 0:06:41
0:06:41
 0:15:40
0:15:40
 0:07:47
0:07:47
 0:09:15
0:09:15
 0:14:02
0:14:02
 0:44:31
0:44:31
 0:58:39
0:58:39
 0:10:07
0:10:07
 0:24:52
0:24:52
 0:56:35
0:56:35
 0:13:15
0:13:15
 0:11:30
0:11:30
 0:18:11
0:18:11