filmov
tv
Worked example: differentiating polar functions | AP Calculus BC | Khan Academy

Показать описание
An AP Calculus sample item where we find the rate of change of _ with respect to _.
AP Calculus BC on Khan Academy: Learn AP Calculus BC - everything from AP Calculus AB plus a few extra goodies, such as Taylor series, to prepare you for the AP Test
For free. For everyone. Forever. #YouCanLearnAnything
Worked example: differentiating polar functions | AP Calculus BC | Khan Academy
Polar functions derivatives | Advanced derivatives | AP Calculus BC | Khan Academy
Worked example differentiating polar functions | Functions | Post Secondary Mathematics
Calculus of Polar Curves: Derivatives & Slopes of Polar Functions
Example: Derivatives in Polar Coordinates
Differentiation of Polar Equations - AP Calculus BC
Finding Area In Polar Coordinates
Calculus 2: Polar Coordinates (6 of 38) Finding the Derivative of a Polar Function
Function of Two Variables:Calculate Directional Derivatives | GATE, CSIR NET, CUET PG, IIT JAM Math
Derivative of Polar Functions | r = 6θ² + 5θ (Example 1)
Derivative of Polar Functions | r = cos²θ + e^5θ (Example 2)
The x partial Derivative in Polar Coordinates
Tangent Line Equations, Slope, & Derivatives In Polar Form | Calculus 2
9.7i Polar Curves, Second Derivative, Example - AP Calculus BC
How To Graph Polar Equations
Find dy/dx of polar functions
Polar Differentiation (AP Calculus)
Polar Derivatives Part 1
Calculus Polar Coordinates - Derivatives
Derivative of Polar Equation (example problem)
When mathematicians get bored (ep1)
Polar Coordinate System
The Derivative (slope of the tangent line) for Polar Functions
8.2 Circular Motion: Position and Velocity Vectors
Комментарии
 0:05:57
0:05:57
 0:09:25
0:09:25
 0:04:20
0:04:20
 0:16:06
0:16:06
 0:07:10
0:07:10
 0:11:05
0:11:05
 0:33:50
0:33:50
 0:03:11
0:03:11
 1:34:25
1:34:25
 0:03:08
0:03:08
 0:05:35
0:05:35
 0:06:59
0:06:59
 0:14:34
0:14:34
 0:00:48
0:00:48
 0:20:33
0:20:33
 0:08:50
0:08:50
 0:23:46
0:23:46
 0:06:16
0:06:16
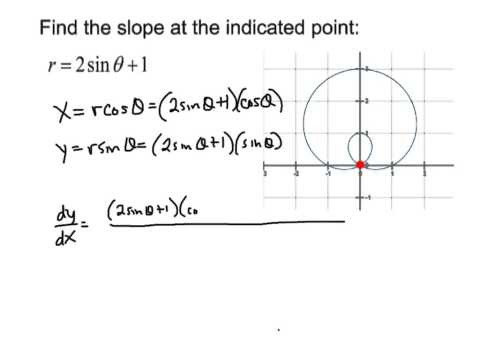 0:08:48
0:08:48
 0:05:22
0:05:22
 0:00:37
0:00:37
 0:04:18
0:04:18
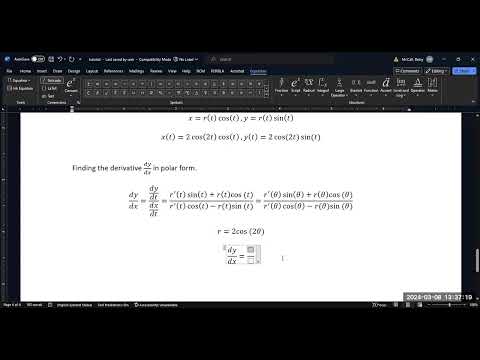 0:10:14
0:10:14
 0:06:02
0:06:02