filmov
tv
Measure Theory 2.4 : Sets of Measure Zero

Показать описание
In this video, I introduce the Cantor Set, and prove that it and countable sets (including the rationals) have measure zero.
Notes : None yet
Notes : None yet
Measure Theory by Paul Halmos #math
Music And Measure Theory
msc semester -third #2023-2024 # mathematics # measure theory
Measure Theory 20 | Outer measures - Part 1
Measure theory, Lecture 06, Definition of Translation and Dilation of a set with Related Theorems
Measurable set II HINDI II MEASURE THEORY II
Measure Theory for Applied Research (Class.4: Measurable Functions)
Measure theory: Cantor set has measure zero but uncountable part 1
Measure Theory
Claudio Landim Measure Theory - Lecture 01: Introduction: A Non-Measurable Set
unit 2 #4 Def of Almost Everywhere Property
Measure Theory for Applied Research (Class.2: Sigma Algebras & Measurable Spaces)
measure and Integration
Measure Theory - Motivation
Measure Theory 21 | Outer measures - Part 2: Examples
How REAL Men Integrate Functions
That's Why Mohit Sir Called 'God Of Mathematics'| Puzzle Brain teaser | #competishun ...
IQ TEST
Measure Theory 1.1 : Definition and Introduction
Measure theory: Sigma-algebra
Measure Theory 17 | Product measure and Cavalieri's principle
Lebesgue Outer Measure or Outer Measure in measure theory | for MSc / MA (mathematics) | higher edu.
Group theory, abstraction, and the 196,883-dimensional monster
Measure Theory -Lec05- Frederic Schuller
Комментарии
 0:00:49
0:00:49
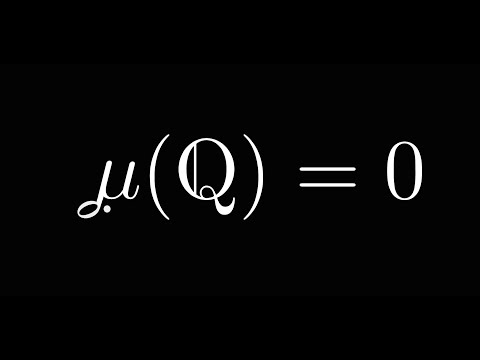 0:13:13
0:13:13
 0:00:15
0:00:15
 0:09:45
0:09:45
 0:14:00
0:14:00
 0:02:47
0:02:47
 0:15:35
0:15:35
 0:05:53
0:05:53
 0:23:10
0:23:10
 0:31:45
0:31:45
 0:05:07
0:05:07
 0:12:17
0:12:17
 0:00:03
0:00:03
 0:14:40
0:14:40
 0:16:48
0:16:48
 0:00:35
0:00:35
 0:00:19
0:00:19
 0:00:29
0:00:29
 0:09:30
0:09:30
 0:26:37
0:26:37
 0:10:28
0:10:28
 0:04:41
0:04:41
 0:21:58
0:21:58
 1:45:50
1:45:50