filmov
tv
Multivariable Calculus | Line integrals over vector fields.

Показать описание
By way of a physical application, we derive the notion of a line integral over a vector field. Some examples are also given.
Introduction to the line integral | Multivariable Calculus | Khan Academy
Evaluating Line Integrals
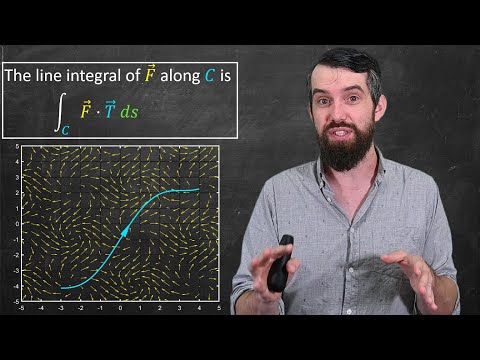
What is a LINE INTEGRAL? // Big Idea, Derivation & Formula
Calculus 3 Lecture 15.3: How to Compute Line Integrals (Over Non-Conservative V.Fields)
Line integral example 1 | Line integrals and Green's theorem | Multivariable Calculus | Khan Ac...
Calculus 3: Line Integrals (18 of 44) What is a Line Integral? [(y)dx+(z)dy+(x)dz] Example 6
Line integrals and vector fields | Multivariable Calculus | Khan Academy
Line Integrals of Vector Fields // Big Idea, Definition & Formula
Line Integrals of Scalar Functions (Introduction)
Line Integrals Practice Problems
Line Integrals Are Simpler Than You Think
How to Evaluate the Line Integral of a Vector Field
Line integral example 2 (part 1) | Multivariable Calculus | Khan Academy
The Fundamental Theorem of Line Integrals // Big Idea & Proof // Vector Calculus
Line Integrals - Evaluating a Line Integral
Vector Calculus - Line Integrals of Vector Field | Example & Solution
Beauty of Line Integral (Calculus) .
Line Integrals. #calculus
Line Integrals in 3D // Formula & Three Applications
Line Integrals with respect to x or y // Vector Calculus
Vector integral calculus: Line integral
Multivariate Calculus (Line Integral) by Irfan Shafqat
Vector Calculus Complete Animated Course for DUMMIES
Calculus 3: How to evaluate line integrals from the definition and parametrization
Комментарии
 0:18:49
0:18:49
 0:12:54
0:12:54
 0:14:02
0:14:02
 2:17:24
2:17:24
 0:13:03
0:13:03
 0:05:03
0:05:03
 0:16:47
0:16:47
 0:08:40
0:08:40
 0:25:29
0:25:29
 0:13:00
0:13:00
 0:21:02
0:21:02
 0:06:16
0:06:16
 0:12:53
0:12:53
 0:06:38
0:06:38
 0:08:24
0:08:24
 0:23:18
0:23:18
 0:08:56
0:08:56
 0:00:51
0:00:51
 0:05:49
0:05:49
 0:11:28
0:11:28
 0:12:02
0:12:02
 0:13:55
0:13:55
 0:46:44
0:46:44
 0:12:58
0:12:58