filmov
tv
ABSOLUTE MAXIMUMS and ABSOLUTE MINIMUMS

Показать описание
How to calculate the absolute extremes of a real function of a real variable f defined on a closed interval, using the Weierstrass extreme value theorem: If a function is continuous and defined in a closed interval, then it has absolute maxima and absolute minima.
Finding Absolute Maximum and Minimum Values - Absolute Extrema
📈 Local and Absolute Maximum and Minimum from a Graph 📈
Absolute Maximum and Minimum Values of Multivariable Functions - Calculus 3
Absolute Maximum and Minimum Values - Finding absolute MAX & MIN of Functions - Calculus
Learn how to find the absolute max, min and relative max min of a graph
Absolute Maximum & Minimum
How to recognize relative and absolute maxima and minima | Functions | Algebra I | Khan Academy
Calculus: Absolute Maximum Minimum for Polynomial First Derivative Application
Use a graph to locate the absolute maximum and absolute minimum
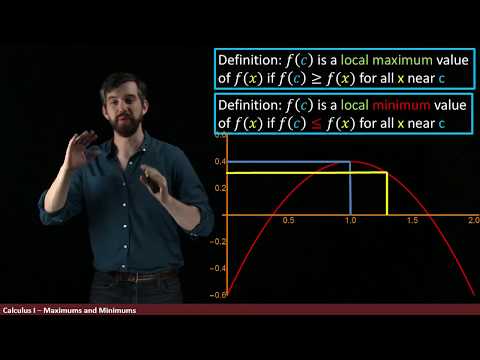
Relative and Absolute Maximums and Minimums | Part I
ABSOLUTE MAXIMUM AND ABSOLUTE MINIMUM
Absolute max and min values Problem 1 (Multivariable Calculus)
Absolute Maximum/Minimum (1 of 2: Domain restricted polynomial)
Absolute minima & maxima (entire domain) | AP Calculus AB | Khan Academy
Local and Absolute Maximum Minimum Differences
Absolute Maximum and Minimum Values of a Function - Calculus I
Use a Graph to Locate the Absolute Maximum and Absolute Minimum | College Algebra
Calc III: Find absolute max/min on a Domain
Find the absolute maximum and absolute minimum values of f on the given interval. ... | Plainmath
Introduction to Absolute Vs Relative Maximums and Minimums
🟡14a - Absolute Minimum and Maximum of Multivariable Functions 1
AP Calculus 4-4 Absolute Maxima and Minima
Absolute Maxima for Trigonometric Function with Boundary Conditions
Absolute max/min over a disc
Комментарии
 0:17:17
0:17:17
 0:03:27
0:03:27
 0:11:24
0:11:24
 0:09:15
0:09:15
 0:02:41
0:02:41
 0:01:00
0:01:00
 0:04:58
0:04:58
 0:05:21
0:05:21
 0:01:44
0:01:44
 0:04:38
0:04:38
 0:16:37
0:16:37
 0:25:26
0:25:26
 0:10:19
0:10:19
 0:09:23
0:09:23
 0:08:34
0:08:34
 0:07:36
0:07:36
 0:05:45
0:05:45
 0:07:42
0:07:42
 0:01:19
0:01:19
 0:06:58
0:06:58
 0:20:02
0:20:02
 0:22:25
0:22:25
 0:05:40
0:05:40
 0:12:37
0:12:37