filmov
tv
A Simple Trigonometric Problem | International Mathematical Olympiad 1963 Problem 5
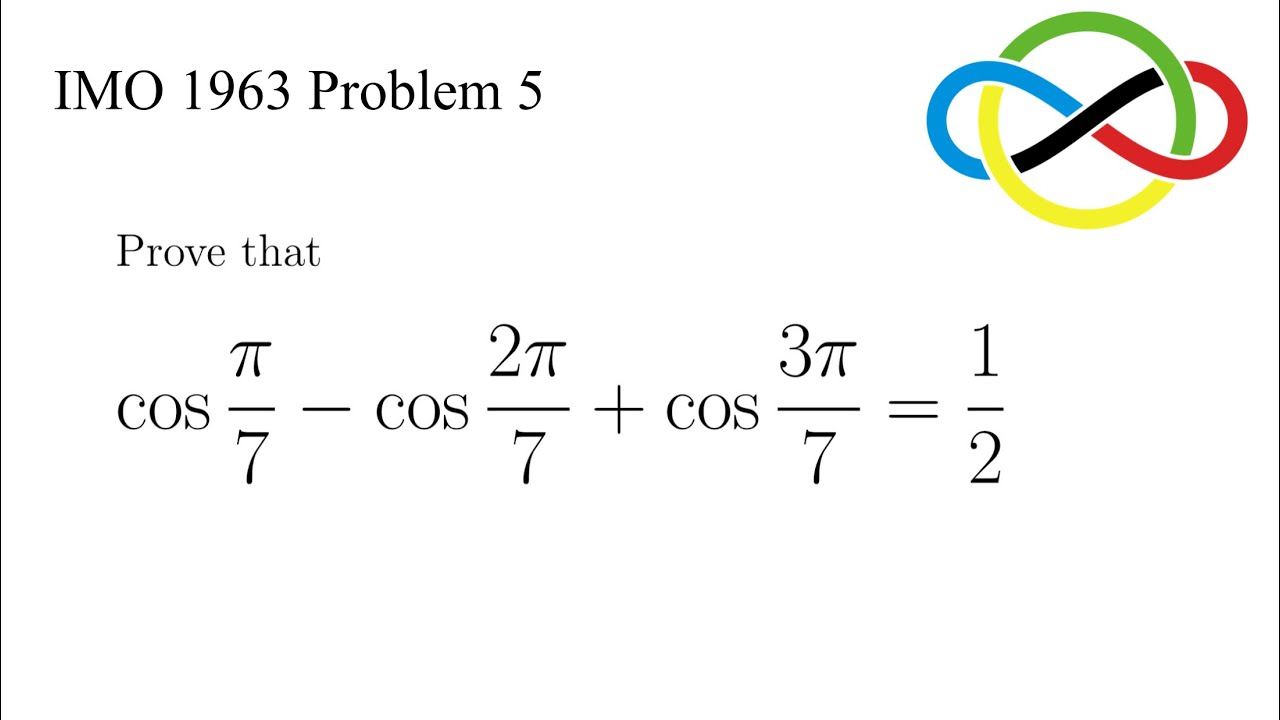
Показать описание
#Math #IMO #Trigonometry
In this video we are going to solve Problem 5 in IMO 1963.
Subscribe @letsthinkcritically !!
————————————————————————————————————————————————
I share Maths problems and Maths topics from well-known contests, exams and also from viewers around the world. Apart from sharing solutions to these problems, I also share my intuitions and first thoughts when I tried to solve these problems.
In this video we are going to solve Problem 5 in IMO 1963.
Subscribe @letsthinkcritically !!
————————————————————————————————————————————————
I share Maths problems and Maths topics from well-known contests, exams and also from viewers around the world. Apart from sharing solutions to these problems, I also share my intuitions and first thoughts when I tried to solve these problems.
A Simple Trigonometric Problem | International Mathematical Olympiad 1963 Problem 5
Missing Side of a Triangle Trigonometry Problem SOH CAH TOA (sin, cos, tan) #shorts #maths #math
Trigonometry For Beginners!
Trigonometry Basics : how to find missing sides and angles easily (6 Golden Rules of SOHCAHTOA)
Simple Trigonometric Problem | Math problems solving | Olympiad math problems | InsaneMaths
A simple trigonometric problem
Trigonometry made easy
How To Solve Two Triangle Trigonometry Problems
Step-by-Step Proof of a Challenging Trigonometric Problem | Simplified Explanation
Random Math Problem 1: Trigonometry
Tips to solve Trigonometric Ratios Problems Fast? | Trigonometry Short Tricks for Competitive Exams
How to Prove Trigonometric Identities (and how not to)
Master Trick to Learn Trigonometric Ratios Value | #mathstricks #mathsshorttricks
Trigonometry: Solving Right Triangles... How? (NancyPi)
how solve trigonometric problems in Casio scientific calculator. short tricks
Solving basic trigonometric problems
The Best Way to Master Trigonometric Identities
Solving Trigonometric Identity EXAMPLE | Pre-Calculus
Solve sin=2/5 Trigonometric equation
Unlock This Trig Identity Trick in Under 60 Seconds!
Trigonometry Funny😂😂😂😂 | #shorts #relatable #cbse #class11 #class12 #class10 #jee
Simple trigonometric problem | trigonometric problem solving | Maths tricks in trigonometry
Simplifying Trigonometric Expressions
Trigonometry Problems on the SAT are Easy Problems
Комментарии
 0:06:06
0:06:06
 0:00:39
0:00:39
 0:21:52
0:21:52
 0:07:24
0:07:24
 0:02:08
0:02:08
 0:01:48
0:01:48
 0:12:43
0:12:43
 0:15:14
0:15:14
 0:06:54
0:06:54
 0:10:59
0:10:59
 0:00:47
0:00:47
 0:07:37
0:07:37
 0:00:59
0:00:59
 0:13:29
0:13:29
 0:00:15
0:00:15
 0:06:42
0:06:42
 0:03:36
0:03:36
 0:00:55
0:00:55
 0:04:04
0:04:04
 0:00:14
0:00:14
 0:00:31
0:00:31
 0:03:32
0:03:32
 0:12:15
0:12:15
 0:00:56
0:00:56