filmov
tv
Solving 3^x+4^x=5^x

Показать описание
Solving this Pythagorean exponential equation 3^x+4^x=5^x
#shorts #pythagorean #algebra
#shorts #pythagorean #algebra
If 3^x + 4^x = 5^x , Find x
Solving 3^x+4^x=5^x
Solve 3(4x+5)=6 , Answer is a Fraction
(x+3)(x+5) Expand and Simplify
Solve 3x + 4 + 5x = 4(2x + 1)
Factoring a quintic x^5+x^4+x^3+x^2+x+1 by grouping
x-4/x-5 + x-6/x-7 = 10/3. Solve the given Equation.
How to solve a 5-term 4th degree polynomial equation x^4+x^3+x^2+x+1=0
Solving Quadratic Equations by Factoring | Finding the Roots | Part 1 |
Solve 3x+4x-5x-6x+8x+7+5-12+6=-8x+2x+80: Linear Equation Video Solution | Tiger Algebra
Expanding Brackets
3/2(x + 4) = 5 – 1/3(4 – x), many don’t know the EASY way to solve!
Linear equation with one unknown: Solve 3x-4+x=5x-6 step-by-step solution
Solving an equation with variables on both side and one solution
x = 4/5 (x + 10) Solve the given equation
Solve 1/5x -3 = 4
5 simple unsolvable equations
2(x + 3) = 5(4x+1) Let’s solve the equation problem step-by-step….
4(x+3) - 3(x+2) Expand and Simplify
Solve the equation x/2 = 3x/4 + 5
Problem 1 Solve linear equation (5x-4)/8 - (x-3)/5 = (x+6)/4
Solve 5x - (2x + 2) = x + (3x - 5) for x
A Nice Exponential Equation (5^x-3^x=16)
Strategies to Solve Multi Step Linear Equations with Fractions
Комментарии
 0:09:15
0:09:15
 0:00:31
0:00:31
 0:01:10
0:01:10
 0:00:44
0:00:44
 0:01:38
0:01:38
 0:02:36
0:02:36
 0:07:07
0:07:07
 0:13:19
0:13:19
 0:27:16
0:27:16
 0:01:43
0:01:43
 0:00:51
0:00:51
 0:26:24
0:26:24
 0:01:39
0:01:39
 0:02:36
0:02:36
 0:00:59
0:00:59
 0:02:54
0:02:54
 0:00:50
0:00:50
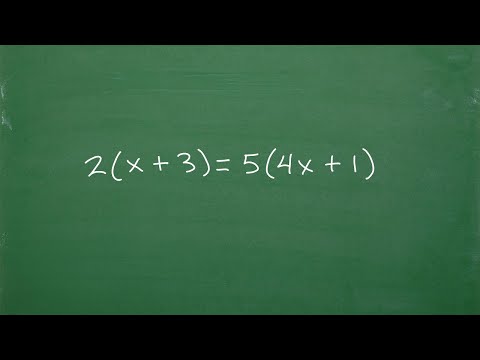 0:17:10
0:17:10
 0:00:42
0:00:42
 0:01:11
0:01:11
 0:03:01
0:03:01
 0:01:25
0:01:25
 0:06:37
0:06:37
 0:15:41
0:15:41