Naïve Bayes Classifier - Fun and Easy Machine Learning

The theory behind the Naïve Bayes Classifier with fun examples and practical uses of it. Watch this video to learn more about it and how to apply it
Want to learn more?
======================================

--------------------------------------------------------------------------------

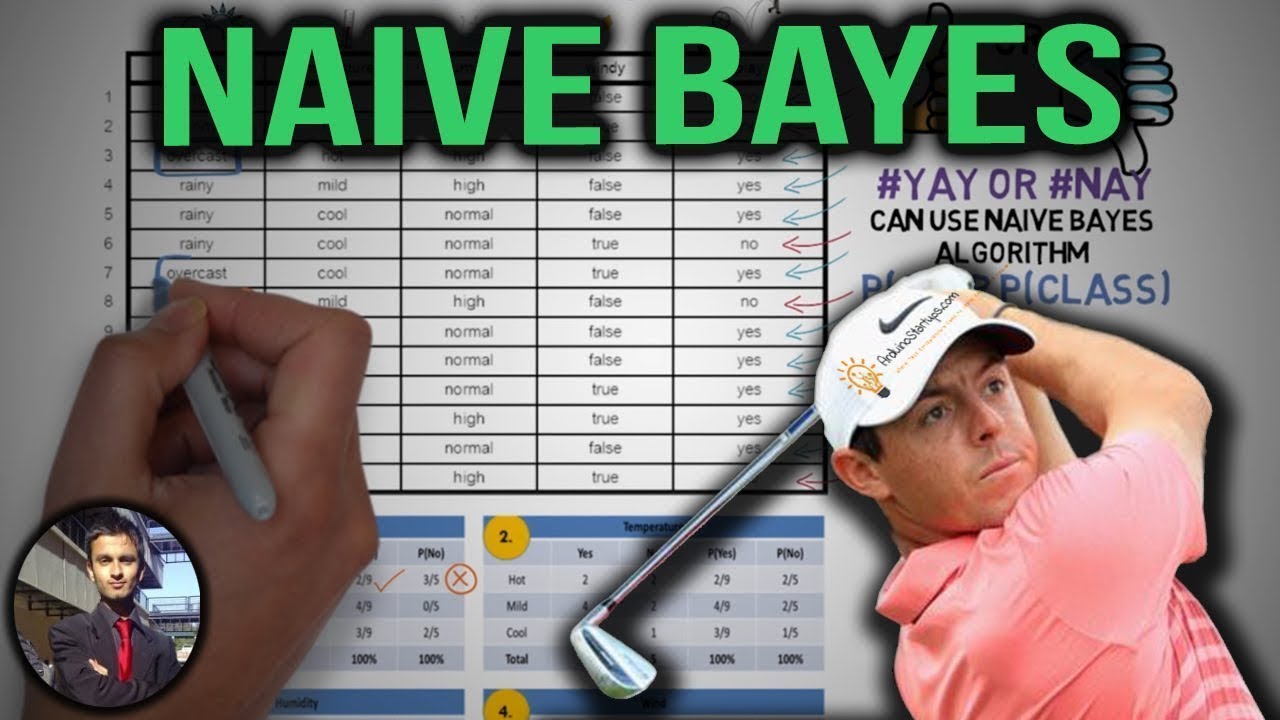
Now Naïve Bayes is based on Bayes Theorem also known as conditional Theorem, which you can think of it as an evidence theorem or trust theorem. So basically how much can you trust the evidence that is coming in, and it’s a formula that describes how much you should believe the evidence that you are being presented with. An example would be a dog barking in the middle of the night. If the dog always barks for no good reason, you would become desensitized to it and not go check if anything is wrong, this is known as false positives. However if the dog barks only whenever someone enters your premises, you’d be more likely to act on the alert and trust or rely on the evidence from the dog. So Bayes theorem is a mathematic formula for how much you should trust evidence.

So lets take a look deeper at the formula,
• We can start of with the Prior Probability which describes the degree to which we believe the model accurately describes reality based on all of our prior information, So how probable was our hypothesis before observing the evidence.

• Here we have the likelihood which describes how well the model predicts the data. This is term over here is the normalizing constant, the constant that makes the posterior density integrate to one. Like we seen over here.

• And finally the output that we want is the posterior probability which represents the degree to which we believe a given model accurately describes the situation given the available data and all of our prior information. So how probable is our hypothesis given the observed evidence.

So with our example above. We can view the probability that we play golf given it is sunny = the probability that we play golf given a yes times the probability it being sunny divided by probability of a yes. This uses the golf example to explain Naive Bayes.
------------------------------------------------------------
Support us on Patreon
Chat to us on Discord
Interact with us on Facebook
Check my latest work on Instagram
Learn Advanced Tutorials on Udemy
------------------------------------------------------------
To learn more on Artificial Intelligence, Augmented Reality IoT, Deep Learning FPGAs, Arduinos, PCB Design and Image Processing then check out

Please Like and Subscribe for more videos :)

[christopherchan]

My professor took several hours to talk about but no idea what he was talking about, I just watched your video just 12 minutes, I fully comprehended. Thank you for guiding how to do my assignment, I was struggling until I watched your video.

[teckyify]

The most important point for NB is that it can be trained incrementally as new evidence comes in. That is a giant drawback in other classifiers in which you have to retrained based on the whole data-set.

[usscork]

Good tutorial, but I'm fairly sure you made a mistake when calculating P(X) to Normalize.

The Value should have been the sum of you initial two equations....0.0053+0.0206 = 0.0259

Then dividing 0.0053/0.0259 = 20.5% for Play = Yes
against 0.0206/0.0259 = 79.5% for Play = No
and these probabilities, collectively adding up to 100% or 1


In your example, you have the probabilities 0.2424 + 0.9421 which is >1 and is just wrong.

Otherwise, as I said... a good and easy to follow tutorial... so thank you.

[groovytau]

Nice video, apparently i understand it better from you than from my teacher, the fact that you use illustrations helps me a lot to visualize the idea and better understand how it works

[ankitshah]

Lot of efforts have been put to create such a nice explanatory video. Thanks a lot for creating such easy to understand video.

[syedshahab]

What an amazing video. If Education system is to changed i would very much like it to become like this.
Enjoyed every second of it. Thanks

[apoorvasrini]

This video was soooo sooo useful to me. I was breaking my head over a bad video from my university course and after watching this it all became soo simple. Keep up the good work!!

[uzKantHarrison]

Not my favorite type of educational video, but I still liked it because it was extremely easy to understand and quite informative.

[GauravKumar-vutd]

Watched for 20 seconds and I knew I had to subscribe immediately if at all i wanted to increase my knowledge! Thanks man! Fantastic video for scums like me who find it hard to understand by reading text book

[asadulhaqmshani]

To beginners (like myself), I suggest you watch this video several times if you don't understand it at first. And also learn about this concept from another source and then come back to this video, it will help you understand more.


Anyway, this is a great video, thanks!

[wajay]

Best Tutorial on Naïve Bayes . Easy to Understand.

[krishnakanjee]

Such an awesome video! You made it look so easy. And your video itself is fun to watch. Thanks!

[FlvckoJr]

wooow, you literally rescued my life 😂😂😂 THANK YOUU SOO MUCH SIR

[SamuelLawson]

Funny thing - I used a Naive Bayes library in Python that attempts to guess whether a statement is positive or negative and gave it two very similar sentences:

"That is a dog."

"That is a cat"

The sentence with 'dog' came back as 67% positive while the sentence with 'cat' was reported as 58% negative
It seems Thomas Bayes preferred dogs! :-D

[ephremtadesse]

it's nice tutorial, just you made it easy to quickly grasp the idea. Thank you!

[kundansahuji]

Awesome video.Finely explained using numerical

[nishkaarora]

this is straght fire i love this video this is how all of ML should be taught kudos <3

[relaxingminds]

really to good and very easy way to teach thank you so much

[jamesturban]

Very great video, this guy is amazing for machine learning

[lizravenwood]

This is the BEST explanation of NB I've ever seen.