filmov
tv
CppCon 2015: Fedor Pikus “C++ Metaprogramming: Journey from simple to insanity and back'
Показать описание
—
—
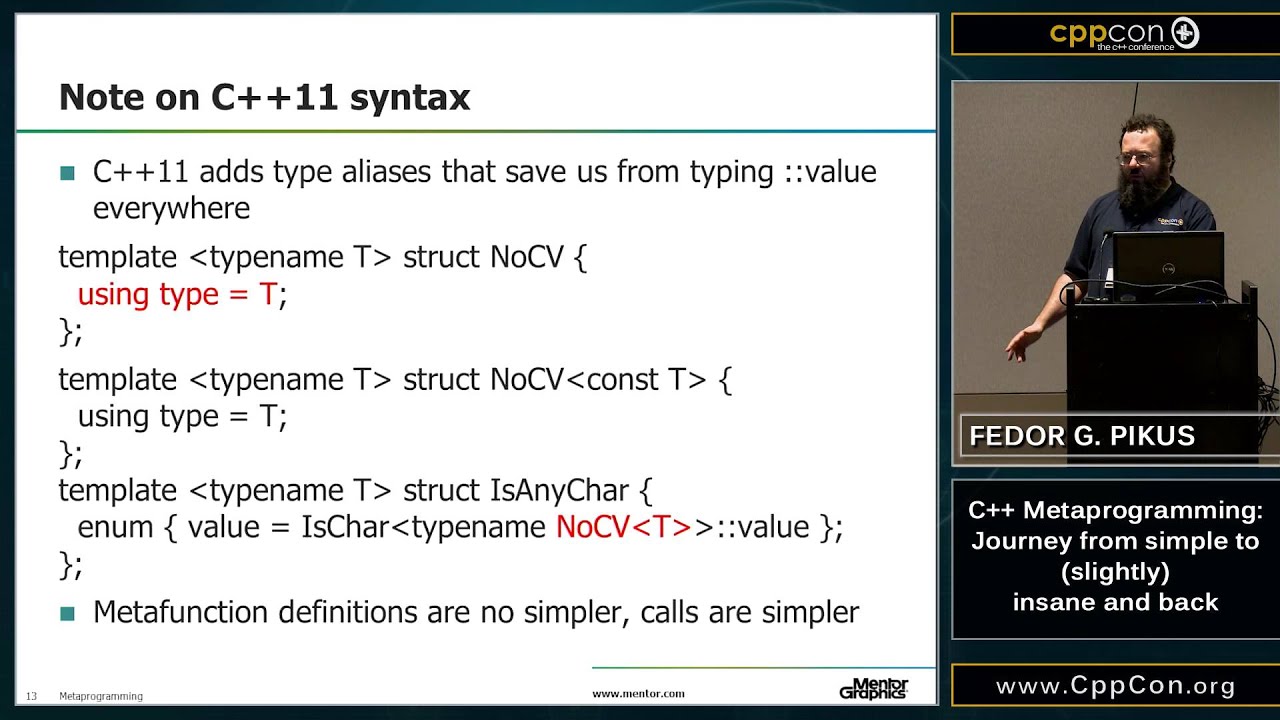
Part I: Introduction to template metaprogramming. Template metaprogramming is a variant of generic programming, a technique that uses C++ template mechanism to perform computations at compilation time, usually to generate, from a single description, executable code that depends on the properties of the data types. It can be viewed as “programming with types”. In this example-driven class we start with the overview of the metaprogramming tools (everything you wanted to know about template specializations but were afraid to ask). We will apply these tools to simple examples, such as: how to sort a sequence in order of increasing values, unless it’s a sequence of pointers, in which case we want the values of what they point to. Part II: Advanced techniques and practical applications. Simple examples of metaprogramming are fun and useful, but once you master them you start chafing at the limitations. This is C++, where we don’t suffer limitations gladly. We therefore move on to the more advanced techniques, including SFINAE, and the appropriately more advanced examples. The journey takes us back to the beginning: after all, when sorting a sequence of values vs a sequence of pointers, you don’t really care whether the pointer is smart or dumb. What you really want to know is whether “*p” compiles or not. What you really need is an “if_compiles” metaprogramming function.
—
Fedor G Pikus is a Chief Engineering Scientist in the Design to Silicon division of Mentor Graphics Corp. His earlier positions included a Senior Software Engineer at Google, and a Chief Software Architect for Calibre PERC, LVS, DFM at Mentor Graphics. He joined Mentor Graphics in 1998 when he made a switch from academic research in computational physics to software industry. His responsibilities as a Chief Scientist include planning long-term technical direction of Calibre products, directing and training the engineers who work on these products, design and architecture of the software, and research in new design and software technologies. Fedor has over 25 patents and over 90 papers and conference presentations on physics, EDA, software design, and C++ language.
—
*-----*
*-----*
—
Part I: Introduction to template metaprogramming. Template metaprogramming is a variant of generic programming, a technique that uses C++ template mechanism to perform computations at compilation time, usually to generate, from a single description, executable code that depends on the properties of the data types. It can be viewed as “programming with types”. In this example-driven class we start with the overview of the metaprogramming tools (everything you wanted to know about template specializations but were afraid to ask). We will apply these tools to simple examples, such as: how to sort a sequence in order of increasing values, unless it’s a sequence of pointers, in which case we want the values of what they point to. Part II: Advanced techniques and practical applications. Simple examples of metaprogramming are fun and useful, but once you master them you start chafing at the limitations. This is C++, where we don’t suffer limitations gladly. We therefore move on to the more advanced techniques, including SFINAE, and the appropriately more advanced examples. The journey takes us back to the beginning: after all, when sorting a sequence of values vs a sequence of pointers, you don’t really care whether the pointer is smart or dumb. What you really want to know is whether “*p” compiles or not. What you really need is an “if_compiles” metaprogramming function.
—
Fedor G Pikus is a Chief Engineering Scientist in the Design to Silicon division of Mentor Graphics Corp. His earlier positions included a Senior Software Engineer at Google, and a Chief Software Architect for Calibre PERC, LVS, DFM at Mentor Graphics. He joined Mentor Graphics in 1998 when he made a switch from academic research in computational physics to software industry. His responsibilities as a Chief Scientist include planning long-term technical direction of Calibre products, directing and training the engineers who work on these products, design and architecture of the software, and research in new design and software technologies. Fedor has over 25 patents and over 90 papers and conference presentations on physics, EDA, software design, and C++ language.
—
*-----*
*-----*
Комментарии
 1:05:58
1:05:58
 0:57:13
0:57:13
 0:38:46
0:38:46
 1:30:21
1:30:21
 1:14:22
1:14:22
 1:03:57
1:03:57
 1:12:04
1:12:04
 1:14:20
1:14:20
 1:00:49
1:00:49
 1:31:21
1:31:21
 1:34:47
1:34:47
 1:00:11
1:00:11
 1:01:52
1:01:52
 1:03:40
1:03:40
 1:03:44
1:03:44
 1:08:11
1:08:11
 1:08:02
1:08:02
 1:29:54
1:29:54
 0:16:26
0:16:26
 0:58:58
0:58:58
 0:48:19
0:48:19
 0:58:23
0:58:23
 0:47:34
0:47:34
 1:03:17
1:03:17