Introduction to the Wasserstein distance

Title: Introduction to the Wasserstein distance

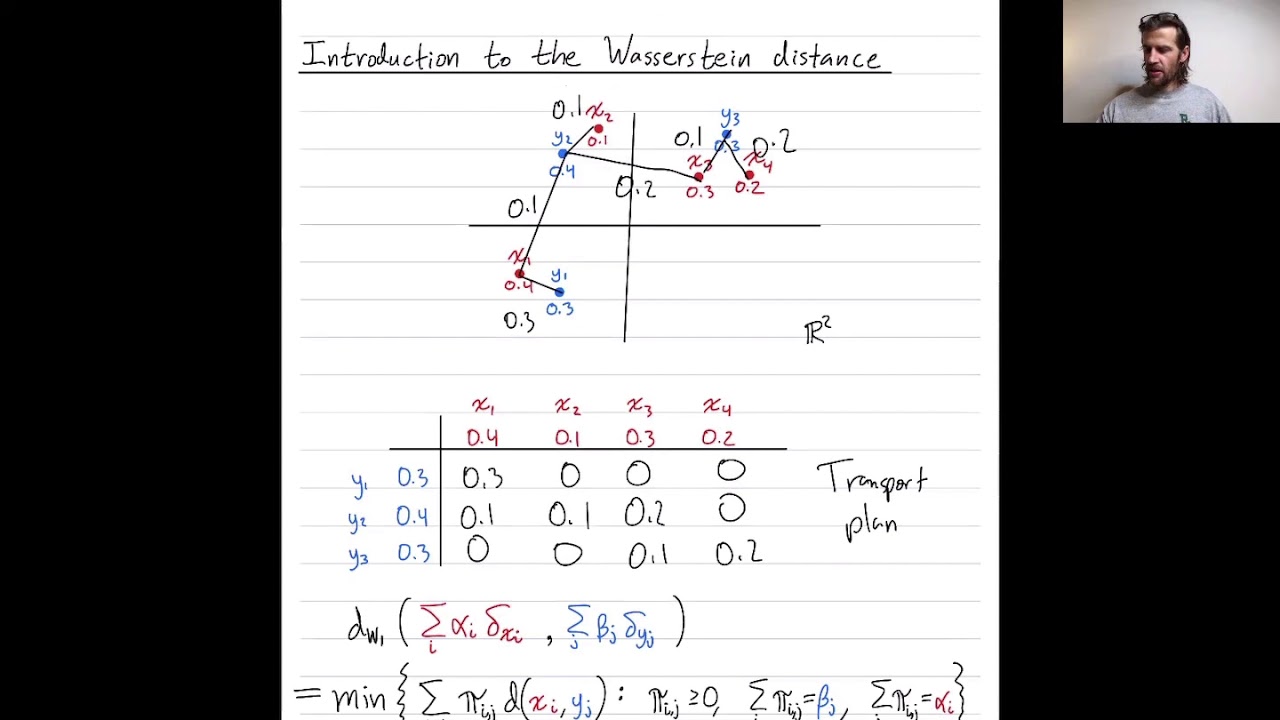
Abstract: I give an introduction to the Wasserstein distance, which is also called the Kantorovich-Rubinstein, optimal transport, or earth mover's distance. In particular, I describe how the 1-Wasserstein distance is defined between probability measures with finite support, and then briefly generalize to measures with arbitrary support. I mention how geodesics with the Wasserstein metric can have much nicer than geodesics with other metrics.

[ThomasFackrell]

This is the first explanation of Wasserstein distance that keeps things intuitive and is not overly hand wavy. The part that helped the most was when you explicitly showed what the transport plan was, how that can be used as a measure, and how Euclidean distance is taken into account.

[rafeedrahman]

This is probably the best explanation of Wasserstein distance available on the internet. Thanks!!

[vnasilva]

You are a GIFTED instructor, your explanation is clear. Thank you!

[zichuanwang]

This is very helpful for me because you write the W distance as an integral, which makes me understand why in the paper there is an expectation in the formula. Also it's amazing to connect the discreate case to transportation problem.

[peilinhe]

Thanks, that's really very helpful. I can finally understand what is measure and how the transport plan emerges. Nice!

[brandomiranda]

if your verbal explanation you say that the wassertein distance if a distance btw probability measure but you are computing a distance between the value of x and y i.e. you are doing d(x, y) instead of d(p(x), p(y)) (the later would be something that KL divergence would be doing). Thus, it makes me think that wassertein distance is more of a distance between **random variable** than on probability measures (which is fine if that's the case). Thus, this makes me think the similarity is more something to what person correlation is doing due to computing a distance between random variables. Can you clarify this point?

[albienchristianaculan]

Thank you for your effort. You have a really great way to explain things!

[Sungjuni]

thank you for your clear and intuitive explanation.

[mohamedrefaat]

Very clear explanation!
At 1:34 you say "in the *smth* norm distance". What is the word that precedes norm distance?

[alexandramalyugina]

Thanks for the explanation, very useful! Do you mind telling which software you use for you notes? Looks simple and awesome, I might give it a try :)

[huyle]

can you suggest some books or notes or references for more theory applications and algorithms of Wasserstein distance?

[OlgaFilippova-kcsb]

Thank you for such a great video! Do you have a video about Maximum Mean Discrepancy?🥺Or can you recommend where to read about it to form intuition what exactly is being measured?

[Rjsipad]

Really good explanation, now I gotta find a video this high quality for the duality!

[jackyman]

finally i understand what Wasserstein Distance is. However, is there any simplistic explanation regarding Kantorovich-Rubistein Duality and Lipschitz condition. Still get confused with those

[mathom]

Thank you very much! Very intuitive. Congratulations!

[RayRay-ytpe]

Thank you so You've just gained a new subscriber

[egekarais]

What an amazing explanation! Very well done.

[raisinbl]

very very very intuitive! Thank you so much

[nalley]

so the distance in the cost function, how is it measured?

[harshvardhan]

nice explanation, if possible please make some more on applications. thanks!