filmov
tv
The Form of the Particular Solution Using the Method of Undetermined Coefficients - Part 1

Показать описание
This video provides examples of how to determine the form of the particular solution to a linear second order nonhomogeneous differential equation. The particular solution is not found.
METHOD OF UNDETERMINED COEFFICIENTS FINDING THE FORM OF THE PARTICULAR SOLUTION
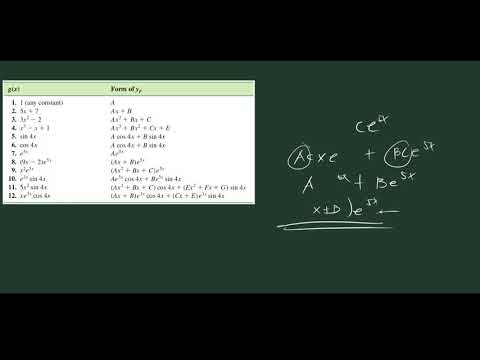
Find the form of the particular solution (y_p) for method of undetermined coefficients
Finding the appropriate form of particular solution in method of Undetermined Coefficients
The Form of the Particular Solution Using the Method of Undetermined Coefficients - Part 1
METHOD OF UNDETERMINED COEFFICIENTS FIGURING OUT THE FORM OF THE PARTICULAR SOLUTION
Determining the general form of a particular solution UNDETERMINED COEFFICIENTS METHOD
Determine the form of a particular solution, sect 4.5#31
Determine the form of a particular solution, second order linear differential equation, sect 4.4 #27
Diff Eqn: finding the correct form for a particular solution, y_p
2214 - 3.8 - Choosing the form of the particular solution
Form of the Particular Solution
Determine the form of a particular solution, second order linear differential equation, sect4.4 #29
Determine the form of a particular solution, second order linear differential equation, sect 4.4#31
C27 Example problem finding the form of the particular solution
Find the appropriate form of particular solution when using method of UC
C26 Example problem finding the form of the particular solution
Differential Equations: How to find the form of the particular part of a non homogenous solution.
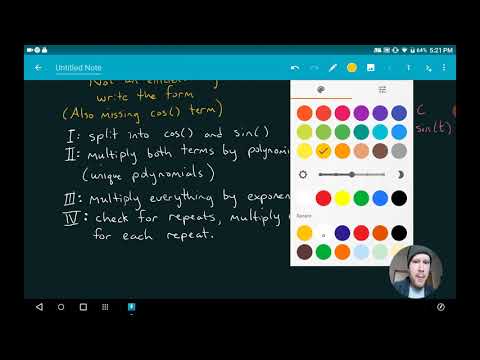
2214 - 3.8 - Form of the Particular Solution when g(t) is Compound
Write form of particular solution yp: 3y'' + 5y' - 2y = 7e^(2t)
The Form of the Particular Solution Using the Method of Undetermined Coefficients - Part 2
Write form of particular solution: y'' + 5y' - 2y = 7e^(-2t)
Write form of particular solution: 3y'' + 5y' - 2y = 7e^(-2t) cos(3t)
Write form of particular solution: 4y'' - 4y' +y = 5e^(3t)
Write form of particular solution: 4y'' - 4y' +y = 5e^(t/2) sin(3t)
Комментарии
 0:09:05
0:09:05
 0:06:05
0:06:05
 0:07:59
0:07:59
 0:07:26
0:07:26
 0:05:46
0:05:46
 0:03:51
0:03:51
 0:07:08
0:07:08
 0:05:13
0:05:13
 0:06:17
0:06:17
 0:36:40
0:36:40
 0:08:51
0:08:51
 0:04:21
0:04:21
 0:05:38
0:05:38
 0:08:11
0:08:11
 0:09:11
0:09:11
 0:06:07
0:06:07
 0:14:59
0:14:59
 0:16:41
0:16:41
 0:00:35
0:00:35
 0:09:15
0:09:15
 0:00:35
0:00:35
 0:00:35
0:00:35
 0:00:35
0:00:35
 0:01:15
0:01:15