Algebraic Topology 11: What is homology measuring?

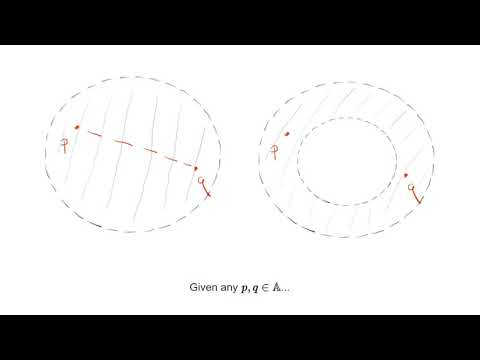
We give the intuition behind homology -- in particular, how homology measures the "holes" of a space of various dimensions. While this motivates the formal definition and helps one understand the calculations, in this lecture we neither give a formal definition or explicit means of calculating homology. For that, see the earlier lecture on simplicial homology or the upcoming lectures on singular homology.

Presented by Anthony Bosman, PhD.

[akashsudhanshu]

Thanos theorem was mind blowing, also this lecture was very important and very well taught. hatts off to you!

[ompatel]

Professor eagerly waiting for next video on singular homology

[albertogilmartinez]

Thank you for these excellent lectures!!!. Will the course cover all the four chapters of the Hatcher's book?

[jackstrider]

Thank you so much for the lucid presentation and explanation. Are you going to cover chapter 3 of Hatcher as well ? If you already did, where can I find the video ?

[giantdad]

The explanation you gave in the beginning about why pi_1 isn't abelian is incorrect and may confuse students. It is clear that a and b^{-1} do not commute because they aren't even loops in the first place, so they don't even represent elements in pi_1. Instead you would have to look at a pair of loops, say ab^{-1} and bc^{-1}, and discuss why they don't commute in pi_1.

[ompatel]

Wooho thank you so much please cover the entire book

[lowerbound]

Such a great lecture!!! Merry Christmas🎅🎅🎅

[DDranks]

Does the definition of a chain imply that the chain can have disconnected components and can have edges with any multiplicity?

[depressedguy]

hey dear sir as promised i am back to the course .

[omprakashjangid]

I am having a doubt at 17:30 For example if I consider simplicial complex spanned by 4 vertices v0, v1, v2, v3, and let vivj denote an oriented edge then the chain v0v1+v1v2+v0v2+2*v2v3-2*v0v3 is a cycle as the boundary is zero but I am not able to see the alpha, beta's etc. in this chain that add to zero that you are talking about at 17:30. Please can you explain. Thanks

[richardchapman]

Slowly absorbing the fundamentals of algebraic topology but wondering if it gets expanded from metrics on rings and links on homeological space to all imaginary spaces much as in arithmetic the integers are generalised through fractions to transcendentals and exhaust real number possibilities. Impatient when ploughing through the definitions and their restrictions so wonder if later there is topology using weirder algebras.

[hyperduality]

Topological holes cannot be shrunk down to zero -- non null homotopic.
The big bang is a Janus point/hole (two faces = duality) -- Julian Barbour, physicist.
"Always two there are" -- Yoda.

[davidhand]

Where did my comment go? I really need an explanation of how these delta complexes are groups. The fundamental group I get; it's the set of loops in a given space that are not equivalent. The Cn and delta n groups seem to be sets of vertices, but what does it _mean?_ Are we still talking about cycles? What is the group's combination operation? What is the inverse of a vertex? I don't get it, please help!

[depressedguy]

I will continue algebraic topology after 2 months right now i am off this topic, i stopped at relative homology and exact sequence long and short both