filmov
tv
Calc 1, Lec 18B: Antiderivatives, Multi Calc (Partial Derivatives: Period & Freq of Mass on Spring)

Показать описание
(0:00) Review content from Lecture 18A (Derivatives of Logarithms and Inverse Tangent (Arctangent)). Show an animation of the graphs of various logarithms (for different bases) and their derivatives.
(2:56) Introduction to antiderivatives (indefinite integrals), including integral notation. Make sure to include the +C ("plus C") in each case for the most general antiderivative. Examples: integrals (general antiderivatives) of 2x, e^(x), -sin(x), and x*cos(x) + sin(x).
(10:06) Harder Example: Suppose F'(x) = 2x*e^(x^2) + x^2*e^(x^2)*2x. The answer is F(x) = x^2*e^(x^2). This must be found by educated guessing, based on the Product Rule and Chain Rule.
(12:24) Introduction to Multivariable Calculus through an example: the period T and frequency f of a harmonic oscillator (a mass on a spring). They are functions of two variables: the mass m and the spring constant k. We can differentiate with respect to either variable. These derivatives are called partial derivatives and the Leibniz notation for them is a slight modification of regular Leibniz notation.
(17:45) Take the partial derivative of T with respect to k and with respect to m. Give the real-life interpretations of the meanings of the signs of these derivatives.
(22:10) Slide showing other partial derivatives (of the frequency f with respect to m and k).
(22:58) Graphs of T and f as functions of m and k in three-dimensional space.
 0:23:52
0:23:52
 0:33:29
0:33:29
 0:33:50
0:33:50
 0:38:44
0:38:44
 0:04:24
0:04:24
 0:30:51
0:30:51
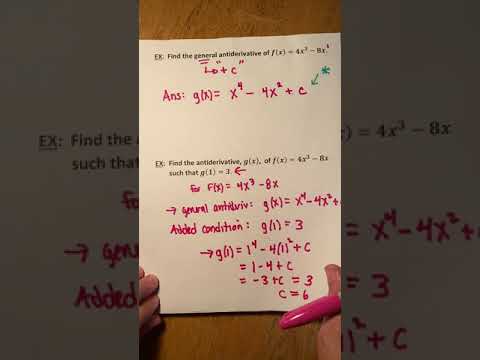 0:23:27
0:23:27
 0:20:22
0:20:22
 0:05:49
0:05:49
 0:00:40
0:00:40
 0:45:00
0:45:00
 0:30:46
0:30:46
 0:06:07
0:06:07
 0:00:23
0:00:23
 0:57:14
0:57:14
 0:07:38
0:07:38
 0:58:17
0:58:17
 0:07:01
0:07:01
 0:57:56
0:57:56
 0:16:23
0:16:23
 0:22:01
0:22:01
 0:38:39
0:38:39
 0:11:35
0:11:35
 0:35:49
0:35:49