filmov
tv
How Ramanujan would DESTROY this tough integral
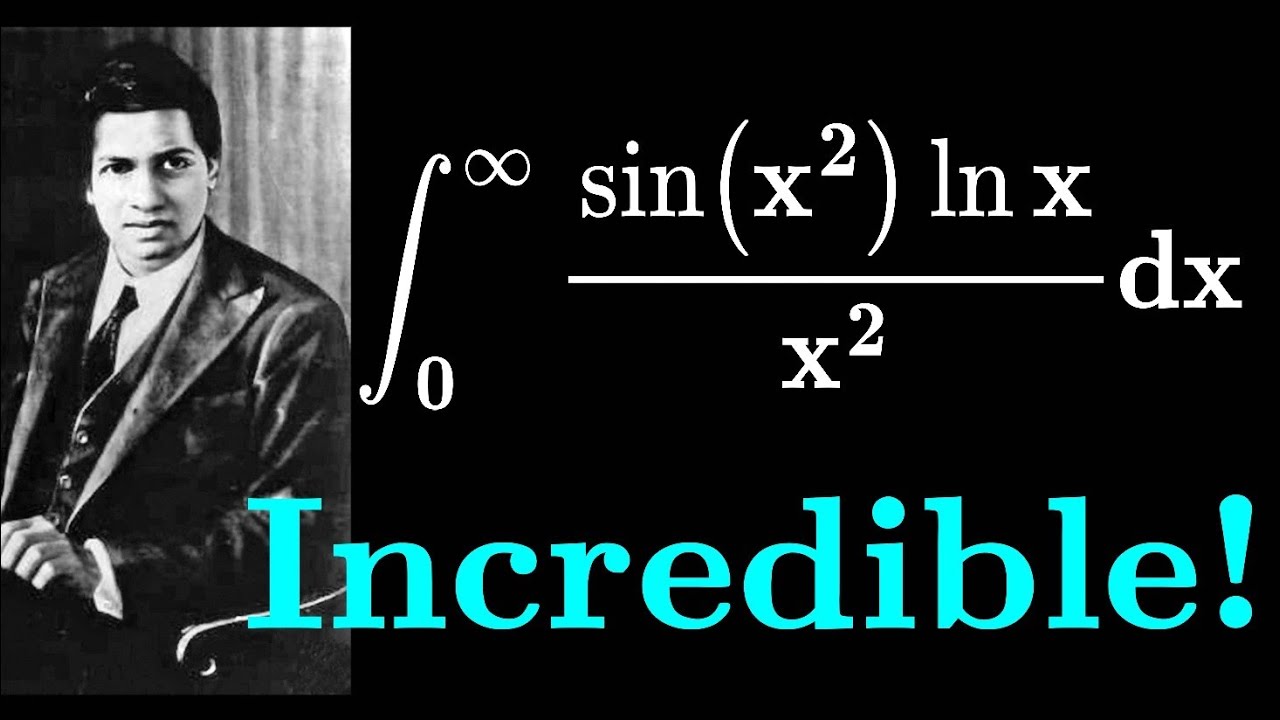
Показать описание
A fascinating integral solved using Feynman's trick and ramanujan's master theorem.
Proof of the master theorem:
My complex analysis lectures:
Support my work and get early access to content via Patreon:
You can follow me on Instagram for write ups that come in handy for my videos and DM me in case you need math help:
My LinkedIn:
Advanced MathWear:
Proof of the master theorem:
My complex analysis lectures:
Support my work and get early access to content via Patreon:
You can follow me on Instagram for write ups that come in handy for my videos and DM me in case you need math help:
My LinkedIn:
Advanced MathWear:
How Ramanujan would DESTROY this tough integral
The highest IQ ever 😲
Bill Gates Vs Human Calculator
Why Haven't You Heard Of One Of History's Greatest Geniuses?
The BEST Argument for the Existence of God
How did Ramanujan solve the STRAND puzzle?
Black Holes Explained
Europe cannot be trusted by Asia - Dr S Jaishankar 😎😎| #shorts
Elon Musk LAUGHS at a Silly Question and Then Gives a BRUTAL but BRILLIANT Answer!
Grant Sanderson (3Blue1Brown): Best Way to Learn Math | AI Podcast Clips
Partitions - Numberphile
Julia Roberts On Hinduism: Neeb Karoli Baba
This Words By Sadhguru Made Audience Speechless😲 |#Shorts #Trending
Human Calculator Solves World’s Longest Math Problem #shorts
Edward Witten Epic Reply 🤣 Destroys String Theory Dissenters
Ramanujan's about facts #oursolarsystem #destroy #shorts
Doctor's Handwritings || Amusing Handwriting ||
15 Year Old YAASHWIN SARAWANAN Is A HUMAN CALCULATOR! | Asia's Got Talent 2019 on AXN Asia
The Simple Question that Stumped Everyone Except Marilyn vos Savant
THIS WAS UNEXPECTED😱😲 | Social Awareness Video By 3rd Eye | #Shorts |#YoutubeShorts
What Made Albert Einstein A Genius?
The Missing Cookie Illusion
India and Nepal United to destroy|| Countries in a nutshell|| #countryballs #shorts #geography
Anyone Can Be a Math Person Once They Know the Best Learning Techniques | Po-Shen Loh | Big Think
Комментарии
 0:12:05
0:12:05
 0:00:56
0:00:56
 0:00:51
0:00:51
 0:18:09
0:18:09
 0:01:00
0:01:00
 0:45:10
0:45:10
 0:01:00
0:01:00
 0:01:00
0:01:00
 0:00:50
0:00:50
 0:03:22
0:03:22
 0:11:45
0:11:45
 0:00:35
0:00:35
 0:00:49
0:00:49
 0:00:34
0:00:34
 0:01:42
0:01:42
 0:00:38
0:00:38
 0:00:15
0:00:15
 0:05:42
0:05:42
 0:07:06
0:07:06
 0:00:41
0:00:41
 0:03:22
0:03:22
 0:00:58
0:00:58
 0:00:38
0:00:38
 0:03:53
0:03:53