filmov
tv
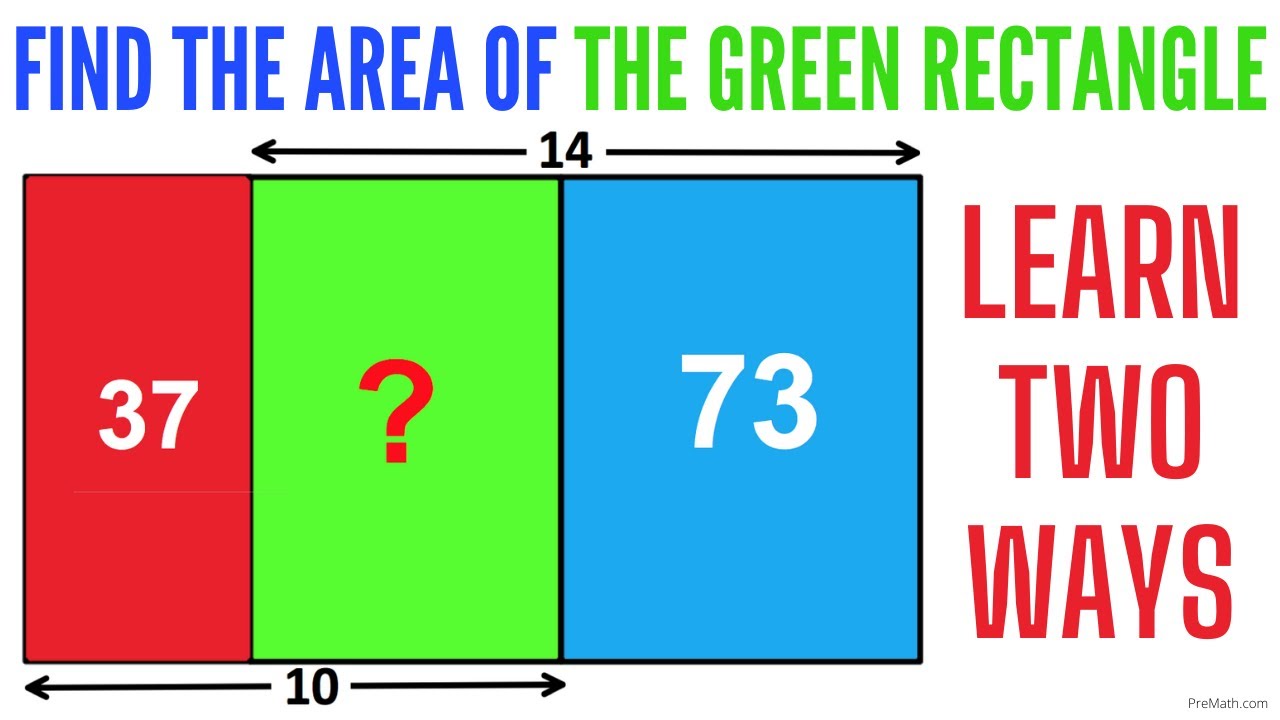
Find Area of the Green Rectangle | Two Methods
Показать описание
Find the Area of the Green Rectangle inside of the Right Triangle | Step-by-Step Tutorial
Find the Area of the Green Rectangle | Step-by-Step Tutorial
Can you find the area of the Green Square? | Circle | (Step-by-step explanation) | #math #maths
Can you find the Area of the Green Shaded Region? | 2 Simple Methods
Find Area of the Green Rectangle | Two Methods
Can you calculate area of the Green shaded region? | (Square) | #math #maths | #geometry
Find the Area of Green, Blue, and Yellow Squares | Quick & Simple Tutorial
Think outside the Box | Find area of the Green shaded Triangle | Important Geometry skills explained
Find the Area of the Green Rectangle Inscribed in a Right Triangle.
What is the area shaded in green?
Calculate area of the Green Square | Blue, Pink, and Yellow Squares | Important skills explained
Can You Find the Green Area in this Square? A Nice Geometry Problem Test Your Math Skills Part 47
Can you find area of the Green shaded region? | (Justify) | #math #maths | #geometry
Can you find the Area of the Green shaded Region? | Quick & Easy Tutorial
Find Area of the Green shaded region | Learn these simple Geometry Tools fast | Math Olympiad
Touching squares problem. Find the area of the green square! (GEOMETRY PROBLEM)
Can you find the Area of the Green Shaded Region? | Double Semicircles
Can you find area of Green triangle in the rectangle? | Easy explanation | #math #maths #mathematics
Can you find area of the Green shaded Square? | (Rectangle) | #math #maths | #geometry
Find the area of the green triangle #mathpuzzles #geometryskills #thinkoutsidethebox #findthearea
Find area of the Green Square | All given shapes are squares| Important Geometry skills explained
Can you find area of the Green shaded region? | (Squares) | #math #maths | #geometry
Olympiad Mathematics | Can you find area of the Green shaded region? | #math #maths
Find the Area of the Green Rectangle | Step-by-Step Explanation
Комментарии
 0:05:29
0:05:29
 0:11:29
0:11:29
 0:11:39
0:11:39
 0:10:49
0:10:49
 0:09:55
0:09:55
 0:09:59
0:09:59
 0:05:42
0:05:42
 0:08:11
0:08:11
 0:02:04
0:02:04
 0:05:47
0:05:47
 0:05:51
0:05:51
 0:09:39
0:09:39
 0:08:29
0:08:29
 0:10:34
0:10:34
 0:06:22
0:06:22
 0:03:53
0:03:53
 0:08:28
0:08:28
 0:12:19
0:12:19
 0:08:11
0:08:11
 0:07:26
0:07:26
 0:08:12
0:08:12
 0:08:52
0:08:52
 0:11:27
0:11:27
 0:06:48
0:06:48