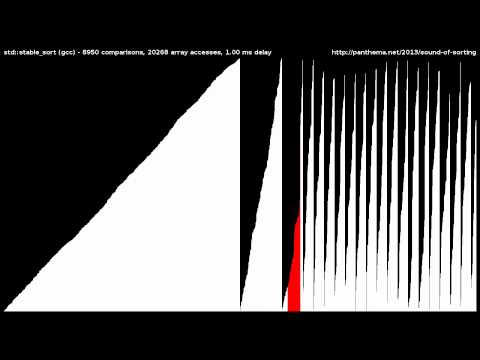
The Bubble Sort Curve

A derivation of the curve that is approximated by a common visualization of the bubble sort diagram.

Music credits:
Night Music by Kevin Macleod
river - Calm and Relaxing Piano Music by HarumachiMusic
... And a couple of my own songs:

Chapters:
00:00 Intro:
0:37 Laying the Background
3:20 How Bubble Sort Works
6:59 Mathematically Describing Diagrams
9:13 Stretching the Diagrams
11:52 Visual Derivation
14:38 Symbolic Derivation
16:48 Nice!
17:07 A Rigorous Solution

[LinesThatConnect]

A few notes which might be of interest, but which didn't fit in the video:

- 3:27 - I'm using a loose pseudocode to represent the algorithm as compactly as possible. The for loops go to N - 2, inclusive. For some reason, that felt more natural to me.

- Most of the list sorting animations use a more optimized version of the algorithm than what I step through. Since the largest n items are sorted after n iterations, we can stop the scan early, so each iteration is quicker than the last one. I used the slower version for the math because it is simpler to pretend that every iteration takes an equal amount of time. To transform the result into the more optimized version, just replace t with 1 - √(1 - t).

- I "cheated" a bit for some of the animations by using specifically designed shuffles to make the curve really clear (0:02, 0:23, 16:54). The curve starts becoming really clear with random shuffles when the size of the list gets into the thousands (like at 2:30). But when the list length is in the low hundreds, it's usually pretty lopsided (like at 1:18). I think the low hundreds size is the most visually pleasing, so I figured that a slightly fudged shuffle was worth the extra visual clarity.

- 1:48 - The timings are actually still not quite right here. The time is based on comparisons only; I forgot to take swaps into account. Insertion sort should be about half as fast as it appears.

[frama]

the curve matching is a lot more satisfying than any sorting video i have seen

[srikar]

The most impressive part of it is that you did not skip the rigor, you wrote up a 26 page paper exploring the details. Really cool video.

[EyalBrown]

You realize you probably have one of the best average video quality on YouTube, right? 4 videos, all killer, no filler.

[bonbondojoe]

Babe not now, factorial guy just dropped

[garthgoldwater]

the way you gray out the inequality and move it to the side, and the way you color and increase or decrease the size of relevant parts of the graphs and equations is SO HELPFUL and i imagine tricky to get exactly right. i really appreciate it

[DavidSartor]

I saw your presentation about this at a conference, maybe a month ago.
I think maybe you said I was the first person you'd met that had seen your videos.

This explanation is much clearer. Thank you.

[Grayson_Wu]

16:22 I can't even imagine the work you put in that ≥ to ≤ transition in manim. Great video as always.

[ndiamantopoulos]

Bro just comes in every year or so and just drops a banger on us

[darkshoxx]

17:50 "Which this epilogue is too small to contain", i.e. it will be proven in 350 years with methods not yet available to us. Here's to hoping 🤞. Great video btw!

[Spiderfffun]

You went this far.. for a sorting algorithim?
Absolutely insane. It was satisfying as hell watching the curve plotted against sorting.

[tingwu_]

This problem has been stuck in my head for a long time. You don't know how surprised and excited I was when I saw this video explaining the exact problem appears in the recommendation! Thank you so much for making this video.

[pietersfilms]

I love the math videos where its not for academic purposes and is just someone talking about and researching something they love. Just started the video but I know im gonna love it, good job

[colindefant]

This is extremely cool! You’re essentially something called a “permuton”. These have become a hot topic over the last several years, but I haven’t seen anyone look at the “bubble sort permuton”.

[Wishbone]

Fantastic video. You found the solution to a "problem" which is utterly useless and would seem to have no practical applications, purely for the joy of discovery and knowledge. And you explained it in a way that even non-mathematicians (i.e. me) can (mostly) understand. Well done, sir. I salute you 🙂

[BadlyOrganisedGenius]

Gorgeous. I always wondered what that curve was approximating, but imagined a proper derivation would be far more complicated than this. You're a smart guy, LTC. Keep it up

[AEastrolabe]

I have been asking myself this very question every now and then for years, but never took the time to look at it closely. I am so glad you made this video and that I found it. Loved it <3

[FutureAIDev]

That final animation of the curve that you found matching the data so smoothly was...jaw-dropping. 😲

[Elesario]

I think the intuitive element of why this shape forms will come from the fact in bubble sort all the larger values will tend to drift to the right more rapidly than the smaller values move left. As you say smaller values will only ever move left once per iteration, but any larger values prior to the largest unsorted value will make multiple moves until the next largest value is found.
From this, because the shape we are perceiving comes from the larger values in any local area, then you'll always get a shape that rapidly climbs to start, and increases more gradually towards it's end.

[dizzylilthing]

0:33 it's called Churgleture and it is a measure of how bigly the datum is