Examples of the Galois Correspondence (Algebra 3: Lecture 21 Video 2)

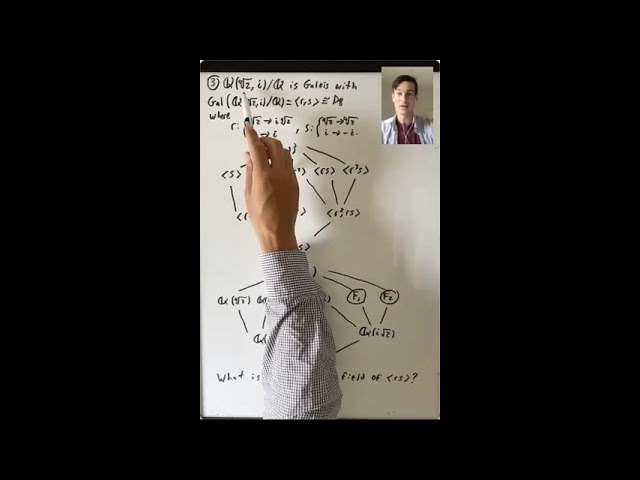
Lecture 21: We started this lecture by proving the one remaining piece of the Fundamental Theorem of Galois Theory.  We then saw some consequences of the fundamental theorem.  We started by returning to some examples we had studied before, including the splitting field of x^3-2 over Q, the splitting field of (x^2-2)(x^2-3) over Q, and the splitting field of x^4-2 over Q.  In this last example, we discussed how to compute the fixed field of a particular subgroup of the Galois group.  
In the second part of the lecture we focused on an important result that we used in the proof of the Fundamental Theorem of Galois Theory that we had not proven yet, Theorem 9 in Section 14.1.  We started by discussing characters of a group G with values in a field L.  We proved a theorem on linear independence of characters and saw what it told us about finite collections of automorphisms of a field K.  We then gave a sketch of the proof of Theorem 9, which involved using our collection of automorphisms, along with collections of elements of our field K, to write down systems of equations.