filmov
tv
Find the 4th Root of (𝟕+√𝟒𝟖) | Olympiad Math
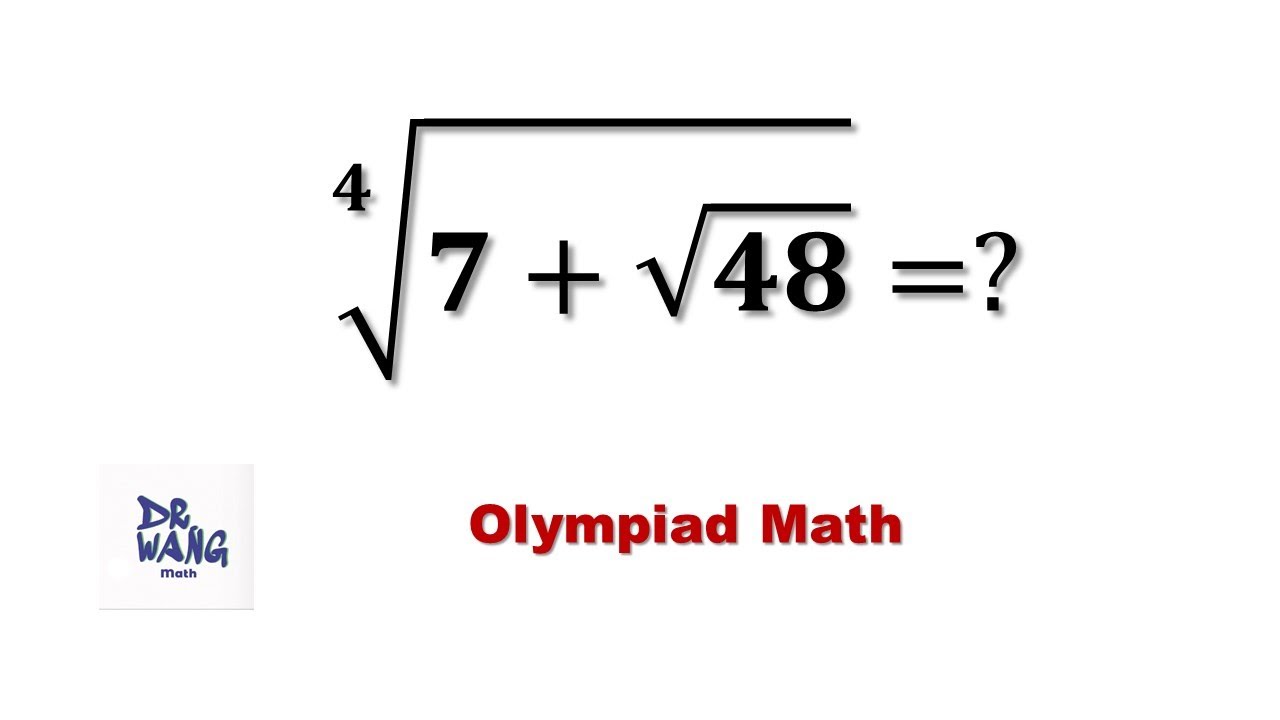
Показать описание
This is a challenging question. The method we use is not common. We define a as the answer. Here are the steps to reach the final answer:
Step 1: Find 1/a. Step 2: Find a^4 + a^(-4) and a^4 - a^(-4). Step 3: Find a^2 + a^(-2) and a^2 - a^(-2).
Step 4: Find a +1/a and a -1/a.
Step 1: Find 1/a. Step 2: Find a^4 + a^(-4) and a^4 - a^(-4). Step 3: Find a^2 + a^(-2) and a^2 - a^(-2).
Step 4: Find a +1/a and a -1/a.
How to find Fourth Root of a Number ∜625
How to Simplify Fourth Roots
4th Root of 5 Digit Numbers II Vedic Math Trick II Calculate Quickly & Accurately #viral #video
4th root of 4 = ??
Find all solutions of the fourth root of -16. De Moivre’s Theorem. Complex roots
Evaluate the Fourth Root of 16
What is the 4th root of 81? Do you remember how to do this?
How to Find the Fourth Roots of a Complex Number, Example with the Fourth Roots of -1
Math 263 F24 Ex 16.7
How to use calculator fx-570ms for square root of 4?
How To Do 4th Roots and 5th Roots On A Casio Calculator (Higher Roots)
How to Find the 4th Root of a Number on the TI 84 Plus CE
Finding the fourth root of an expression to higher powers, fourth root
find the fourth roots
Fourth Root Tricks And Magic | How To Solve The Fourth Root Of A Number | #surajmathematics #short
How to Find Fourth Root of a Number
find the value of (-i)^(1/4), the fourth root of -i
How to find Fourth Root ?
Simplify fourth root|How to find fourth root of a number|Fourth root of a number|Fourth root
Find the 4th Root of (𝟕+√𝟒𝟖) | Olympiad Math
approximate 4th root of 75, Newton's Method, calculus 1 tutorial
Learn how to take the fourth root of a variable expression, fourth root
What is the cube root of 64? #math #tutor #mathtrick #cuberoot #exponents #indices #fraction
is the square root of i the same as fourth root of -1?
Комментарии
 0:00:58
0:00:58
 0:06:31
0:06:31
 0:07:25
0:07:25
 0:00:08
0:00:08
 0:06:22
0:06:22
 0:00:38
0:00:38
 0:00:16
0:00:16
 0:07:55
0:07:55
 2:03:41
2:03:41
 0:00:15
0:00:15
 0:01:43
0:01:43
 0:00:51
0:00:51
 0:04:10
0:04:10
 0:04:29
0:04:29
 0:00:20
0:00:20
 0:03:46
0:03:46
 0:04:05
0:04:05
 0:00:48
0:00:48
 0:03:13
0:03:13
 0:10:52
0:10:52
 0:05:55
0:05:55
 0:01:44
0:01:44
 0:00:50
0:00:50
 0:01:10
0:01:10