filmov
tv
exact value of sin(3 degrees)

Показать описание
In this video, we will find the exact value of sin(3 degrees). We will see the special special triangles and the angle difference formula! ft. sin(15), sin(18), cos(15), cos(18)
exact value of sin(3 degrees)
The Exact Value for Sine of 3 Degrees, sin(3)
I found the exact value of sin 1 degree (from sin 3 degrees) | Inspired by @blackpenredpen
Calculating the exact value of sin 3
find exact values of sin and cos 3
The Exact Value of sin 3 degrees.
sin(3 degrees) via small-angle approximation
How do you find the exact value of sin(3π/4)?
PC Activity 23 Pt. 1 - Exact Values using Sum & Difference Identities
exact value of sin(10 degrees)
Find the exact value of sin(-4π/3) trigonometric function six different ways
How To Use Reference Angles to Evaluate Trigonometric Functions
Trick for doing trigonometry mentally!
Find the exact value of sin(10𝜋/3)
How To Find The Exact Values of Trig Functions
Trig: Finding the exact value of cos (2 inv sin 3/5)
How To Find The Exact Value of the Five Remaining Trigonometric Functions
Finding the EXACT Values for sin(10), sin(50), and sin(70) Using the Cubic Formula
The Exact Value for Sine of 51 Degrees, sin(51)
The Exact Value of sin 33 degrees.
The Exact Value for Sine of 66 Degrees, sin(66)
Find exact value for sin(2 sin^(-1) sqrt(3)/2. Double Angle Formula
The exact values for sin and cos 0, 30, 45, 60 and 90
Trigonometry: Exact value of sin 15
Комментарии
 0:33:16
0:33:16
 0:06:04
0:06:04
 0:11:28
0:11:28
 0:10:00
0:10:00
 0:02:00
0:02:00
 0:04:31
0:04:31
 0:02:22
0:02:22
 0:04:45
0:04:45
 0:16:51
0:16:51
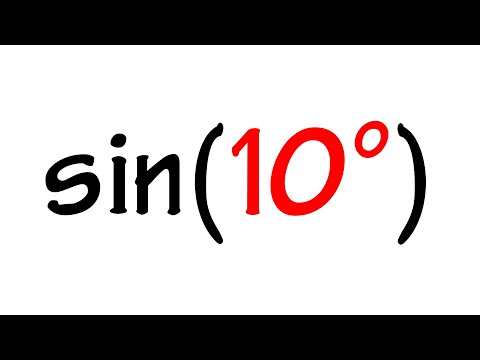 0:20:20
0:20:20
 0:10:31
0:10:31
 0:10:59
0:10:59
 0:05:02
0:05:02
 0:07:08
0:07:08
 0:12:39
0:12:39
 0:02:57
0:02:57
 0:07:11
0:07:11
 0:13:32
0:13:32
 0:06:02
0:06:02
 0:04:28
0:04:28
 0:04:42
0:04:42
 0:02:07
0:02:07
 0:06:14
0:06:14
 0:02:07
0:02:07