filmov
tv
Measure Theory - 1: Geometric and Intuitive Ideas -1

Показать описание
The first three in this series try to give some intuitive and geometric ideas underlying the theory Lebesgue measure. Viewers who are too formal and who believe that any statement in mathematics should be rigorous are requested to skip these three videos! Like any new idea, measure theory also starts with vague questions, still more vague answers and as one goes along one makes them more precise.. I try to exhibit the agonizing thought process (not necessarily of the creator of the theory, Lebesgue) as I went through this while learning and then teaching to my classmates and students later.
Do not aim for 100% understanding. Try to get the ideas and think over them. My students who did this actually claimed that measure theory was an easy one! Can you believe this? Give it a try.
I dedicate this series to Professor Bhaba Sarma, IITG who has been editing all my 350+ videos. Without his enthusiastic help and conviction that this channel will help students of Mathematics, I could not have gone this far.
I also thank the members of the MTTS Trust who share Bhaba's conviction and lent their support for this channel in various form such as recommending it to their students and audience of their lectures.
Finally, I thank those who persuaded me to start the series on Measure theory. Hope they like these videos.
Timestamp:
00:00 Introduction
0:54 Aim of the lecture
2:05 About email and list of videos
4:22 What does measure theory mean?
7:18 Review of Riemann integration
20:11 Riemann integration in terms of step function
21:50 Difference b/w R.D and lebesgue
27:02 Some advice
30:35 Difficulty in defining measure in Dirichlet's function
35:18 Measure in n-dim subsets
57:24 What we did and will do in upcoming videos
58:35 Outro
Music I use: Bensound
License code: BGVUHKIWPLP92UKG
Do not aim for 100% understanding. Try to get the ideas and think over them. My students who did this actually claimed that measure theory was an easy one! Can you believe this? Give it a try.
I dedicate this series to Professor Bhaba Sarma, IITG who has been editing all my 350+ videos. Without his enthusiastic help and conviction that this channel will help students of Mathematics, I could not have gone this far.
I also thank the members of the MTTS Trust who share Bhaba's conviction and lent their support for this channel in various form such as recommending it to their students and audience of their lectures.
Finally, I thank those who persuaded me to start the series on Measure theory. Hope they like these videos.
Timestamp:
00:00 Introduction
0:54 Aim of the lecture
2:05 About email and list of videos
4:22 What does measure theory mean?
7:18 Review of Riemann integration
20:11 Riemann integration in terms of step function
21:50 Difference b/w R.D and lebesgue
27:02 Some advice
30:35 Difficulty in defining measure in Dirichlet's function
35:18 Measure in n-dim subsets
57:24 What we did and will do in upcoming videos
58:35 Outro
Music I use: Bensound
License code: BGVUHKIWPLP92UKG
Комментарии
 0:59:08
0:59:08
 1:02:32
1:02:32
 0:17:24
0:17:24
 0:14:55
0:14:55
 0:57:45
0:57:45
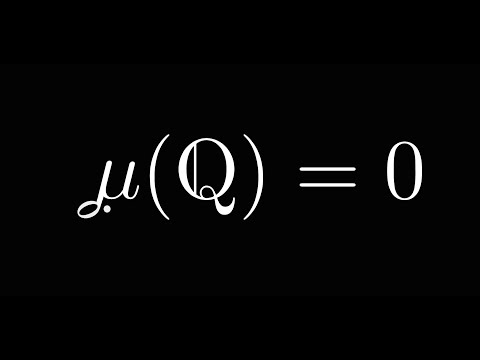 0:13:13
0:13:13
 1:09:07
1:09:07
 1:24:46
1:24:46
 0:01:00
0:01:00
 0:00:38
0:00:38
 0:08:16
0:08:16
 0:00:49
0:00:49
 2:36:21
2:36:21
 0:20:09
0:20:09
 0:04:56
0:04:56
 0:00:15
0:00:15
 0:25:58
0:25:58
 0:50:28
0:50:28
 0:20:46
0:20:46
 0:00:35
0:00:35
 0:22:38
0:22:38
 0:00:46
0:00:46
 2:41:21
2:41:21
 0:50:15
0:50:15