filmov
tv
numerical integration with variable limits in python

Показать описание
numerical integration with variable limits in python
numerical integration is a technique to calculate the integral of a function when an analytical solution is difficult or impossible to obtain. python offers several libraries to perform numerical integrations, such as numpy and scipy. in this tutorial, we will focus on using the scipy library, which provides a convenient function for numerical integration.
1. installing required libraries
if you haven't already installed scipy and numpy, you can do so using pip:
2. understanding the basics
numerical integration can be performed using various methods, including:
- trapezoidal rule
- simpson's rule
- adaptive quadrature methods
3. using the `quad` function
the `quad` function integrates a function of one variable between two given limits. the syntax is as follows:
where:
- `func` is the function to integrate.
- `a` is the lower limit of integration.
- `b` is the upper limit of integration.
- `result` is the computed integral.
- `error` is an estimate of the absolute error in the result.
4. example: numerical integration with variable limits
let's say we want to integrate the function \( f(x) = x^2 \) from variable limits \( a \) to \( b \). in this example, we will create a function to perform the integration and allow the user to input the limits.
code example
explanation of the code
2. **define the function**: we define the function `integrand(x)` that returns \( x^2 \).
3. **integration function**: we create a function `integrate_function(a, b)` that takes lower and upper limits as input and returns the result and estimated error of the integration.
4. **main execution**:
- the user is prompted to enter the lower and upper limits.
- ...
#NumericalIntegration #PythonProgramming #numpy
numerical integration
variable limits
Python
scipy
quad function
trapezoidal rule
Simpson's rule
numerical methods
definite integrals
integration techniques
function approximations
computational mathematics
python libraries
numerical analysis
adaptive quadrature
numerical integration is a technique to calculate the integral of a function when an analytical solution is difficult or impossible to obtain. python offers several libraries to perform numerical integrations, such as numpy and scipy. in this tutorial, we will focus on using the scipy library, which provides a convenient function for numerical integration.
1. installing required libraries
if you haven't already installed scipy and numpy, you can do so using pip:
2. understanding the basics
numerical integration can be performed using various methods, including:
- trapezoidal rule
- simpson's rule
- adaptive quadrature methods
3. using the `quad` function
the `quad` function integrates a function of one variable between two given limits. the syntax is as follows:
where:
- `func` is the function to integrate.
- `a` is the lower limit of integration.
- `b` is the upper limit of integration.
- `result` is the computed integral.
- `error` is an estimate of the absolute error in the result.
4. example: numerical integration with variable limits
let's say we want to integrate the function \( f(x) = x^2 \) from variable limits \( a \) to \( b \). in this example, we will create a function to perform the integration and allow the user to input the limits.
code example
explanation of the code
2. **define the function**: we define the function `integrand(x)` that returns \( x^2 \).
3. **integration function**: we create a function `integrate_function(a, b)` that takes lower and upper limits as input and returns the result and estimated error of the integration.
4. **main execution**:
- the user is prompted to enter the lower and upper limits.
- ...
#NumericalIntegration #PythonProgramming #numpy
numerical integration
variable limits
Python
scipy
quad function
trapezoidal rule
Simpson's rule
numerical methods
definite integrals
integration techniques
function approximations
computational mathematics
python libraries
numerical analysis
adaptive quadrature
 0:19:28
0:19:28
 0:03:34
0:03:34
 0:06:19
0:06:19
 0:10:07
0:10:07
 0:00:35
0:00:35
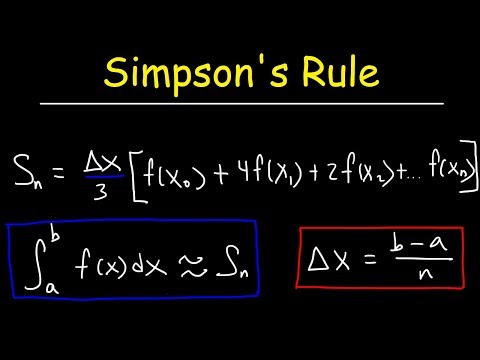 0:12:11
0:12:11
 0:03:01
0:03:01
 0:15:29
0:15:29
 0:34:06
0:34:06
 0:00:52
0:00:52
 0:12:23
0:12:23
 0:10:26
0:10:26
 0:06:41
0:06:41
 0:14:52
0:14:52
 0:00:59
0:00:59
 0:08:00
0:08:00
 0:00:09
0:00:09
 0:16:20
0:16:20
 0:22:30
0:22:30
 0:00:06
0:00:06
 0:31:57
0:31:57
 0:15:29
0:15:29
 0:20:29
0:20:29
 0:00:51
0:00:51