Proof: Lengths of two tangents from an external point to a circle are equal #shorts

Показать описание

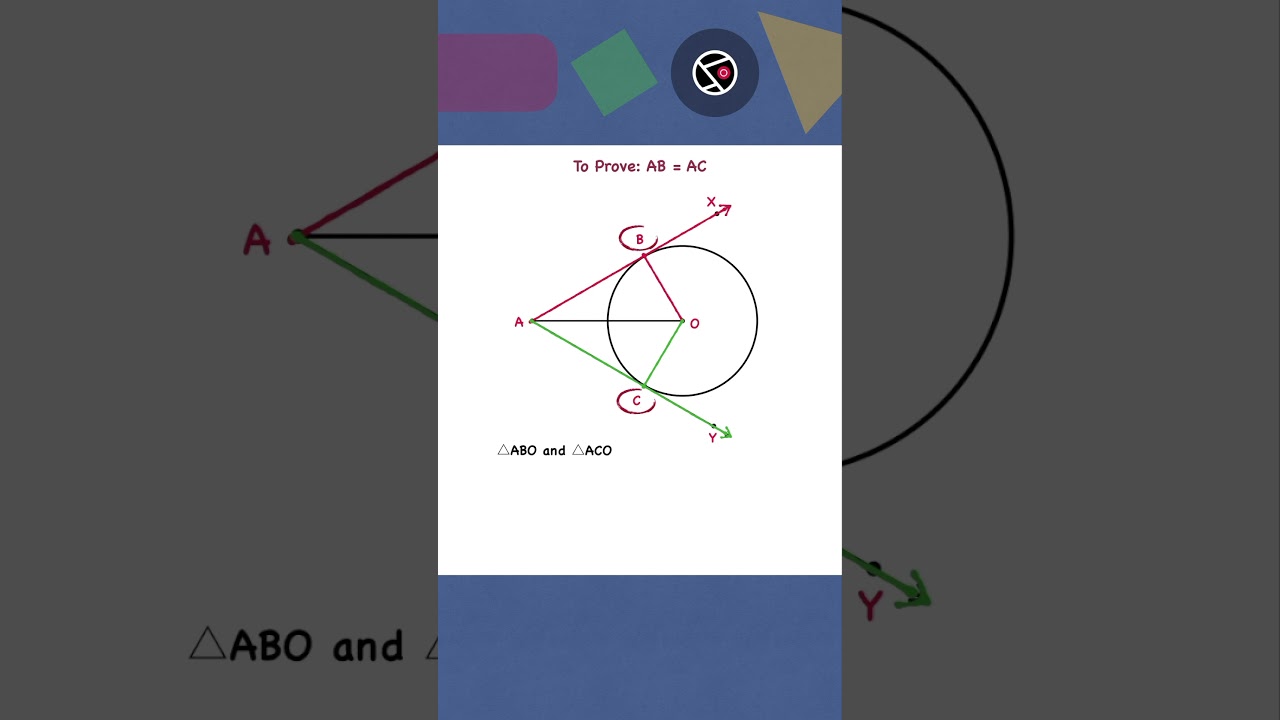
If we draw two tangents from an external point to a circle, the lengths of these two tangents are equal. This can be proved by using the following concepts:
1. All radii of the circle are equal
2. A tangent to a circle is perpendicular to the radius of the circle at the point of tangency.
3. Two triangles are congruent if they satisfy the RHS criterion of congruency
- R: Both are right angled triangles
- H: Both have equal hypotenuses
- S: Besides hypotenuse, there is another pair of equal corresponding sides

Alternate Description
The tangents drawn from an external point to a circle are equal.
The lengths of tangents drawn from an external point to a circle are equal.
Tangent segments from a single point to a circle at different points are equal.

#circle #tangents #geometry

Рекомендации по теме

Комментарии

Plzz do many videos like this sir!! Thank u 🥰💛

ranjini.c

Thank you now I might pass my final tomarrow 💀

To any math teachers reading this, just link videos like this. Not long explanations, just shorts. Very easy to understand as a 16 yr old

Janxaa

Thank you very much! One question: how do we know that the angles ABO and ACO are 90 degrees?

alittax

Proof: Lengths of two tangents from an external point to a circle are equal #shorts

Proof: Lengths of two tangents from an external point to a circle are equal #shorts

Proof: Segments of two tangents to a circle are equal length

Two Tangents Theorem Proof

proof of two tangents drawn from external point to a circle are equal in length grade10l#shorts

Class10th – Equal Tangents from an External Point Theorem | Circles | Tutorials Point

Prove that the lengths of two tangents drawn from an external point to a circle are equal.

Find arc intercepted by two tangents

Circle theorems - two tangents are equal

Prove that the lengths of two tangents drawn from an external point to a circle are equal. #shorts

Circles - 11. Lengths of two tangents drawn from external point to a circle are SAME

Prove that 'the lengths of tangents drawn from an external point to a circle are equal'#ss...

Prove that the length of two tangents drawn from an external point a circle are equal.

Determine the value of x when given two tangent lines to a circle

Circle Theorem Proofs: Two tangents from the same point are equal in length

Prove that, the lengths of two tangents drawn from an external point to a circle are equal #CBSE10

Prove that the length of two tangents drawn from an external point to a circle are equal

Prove that tangents drawn from an external point to a circle are equal || class 10th || triangles.

to prove the length of two tangents drawn from an external point are equal (class 10 circle)

Tangents from an external point to a circle | construction of tangents to a circle

Power Theorems - Chords, Secants & Tangents - Circle Theorems - Geometry

Proof of two tangents drawn from external point to a circle are equal in lengthl#vijayyadavyadav1415

Prove that the angle between the two tangents drawn from an external | Exercise 10.2 [Q10]

Two tangents drawn to a circle from a point outside it are equal in length |

Proving lengths of tangents drawn from external point to a circle are equal