37. Prove that lim⁡(x→a) √x=√a if a≻0. [Hint: Use |√x-√a|=|x-a|/(√x-√a).]

preview_player
Показать описание
37. Prove that lim⁡(x→a) √x=√a if a≻0. [Hint: Use |√x-√a|=|x-a|/(√x-√a).]

Calculus: Early Transcendentals
Chapter 2: Limits and Derivatives
Section 2.4: The Precise Definition of a Limit
Problem 37

7/1/2024 - 3,419 Subscribers - 771,246 Views
  1. The SAT Tutor
  2. Homework
  3. Homework Help
  4. Problem Walkthrough
  5. SAT Tutor
  6. SAT
Рекомендации по теме
37. Prove that 0:05:11

37. Prove that lim⁡(x→a) √x=√a if a≻0. [Hint: Use |√x-√a|=|x-a|/(√x-√a).]

Prove the limit 0:14:18

Prove the limit statements in Exercises 37–50

Human Calculator Solves 0:00:34

Human Calculator Solves World’s Longest Math Problem #shorts

#Trigonometry all formulas 0:00:16

#Trigonometry all formulas

Deriving e from 0:06:33

Deriving e from the limit (1+1/x)^x as x approaches infinity

The Limit (do 0:12:08

The Limit (do not use L'Hospital rule)

Example - Epsilon 0:05:09

Example - Epsilon Delta Definition of Limit | L38 | Intro Complex @ranjankhatu

When mathematicians get 0:00:37

When mathematicians get bored (ep1)

Find the One-Sided 0:00:45

Find the One-Sided Limit with Absolute Value: |x|/x as x approaches zero from the Left #shorts

Suppose limx➡️4 ƒ(x) 0:01:44

Suppose limx➡️4 ƒ(x) = 0 and limx➡️4 g(x) = -3. Find (a)limxS➡️4(g(x) + 3) (b)limx➡️4xƒ(x)...

NEWYES Calculator VS 0:00:14

NEWYES Calculator VS Casio calculator

limit 1+1/f(x)^g(x)=e^g(x)/f(x) Proving 0:03:15

limit 1+1/f(x)^g(x)=e^g(x)/f(x) Proving Limit Formula?

Piecewise Functions - 0:10:06

Piecewise Functions - Limits and Continuity | Calculus

Use formal definitions 0:05:37

Use formal definitions to prove the limit statements in Exercises 89–92.

Cheating in exams😏!? 0:00:32

Cheating in exams😏!?

Limits With Epsilon-delta 0:58:59

Limits With Epsilon-delta definition! (9 examples) | Practice Problems | Calculus I

Tough times Never 0:00:22

Tough times Never last 😊✌️ #delhipolice #motivation

UPSC VS IIT 0:00:14

UPSC VS IIT JEE 🥵 #iitstatus #motivation #toppers #iitjee #jeemains #upscstatus #neet #nit #jee

IIT Bombay CSE 0:00:11

IIT Bombay CSE 😍 #shorts #iit #iitbombay

Most💯 Important Step 0:00:16

Most💯 Important Step Before any Procedure 🔥

25. Prove the 0:01:37

25. Prove the statement using the ε, δ definition of a limit. (lim⁡)(x→0)x^2=0

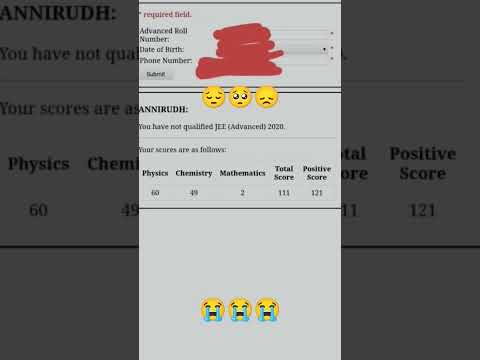
😭A student who 0:00:13

😭A student who didn't qualify jee advanced| subject wise cutoff not clear | #iit #jeemains #jee...

Limit of 1/(2x 0:00:30

Limit of 1/(2x + 3) as x Approaches Infinity #shorts

How to Find 0:00:30

How to Find the Limit of cos(x) as x Approaches Infinity #shorts

Комментарии
Автор

So there are two corrections, firstly, you replace the 1 by, say, (a/2) and then get an upper bound for the denominator. Then you get the delta value the same way you did. Now, you have to take the minimum of this delta value and (a/2), to ensure that all your inequalities will hold.

literallyjustayoutubecomme
Автор

Hmm, the hint here is incorrect, the one in the thumbnail is correct. The proof is anyway incorrect, you assume implicitly that a\geq 1, which is not necessarily true. You can only assume that it is greater than some positive number, since it is positive, then work with that

literallyjustayoutubecomme