The Rational Numbers Are Not So 'Rational' | Everywhere but Nowhere, Part 1

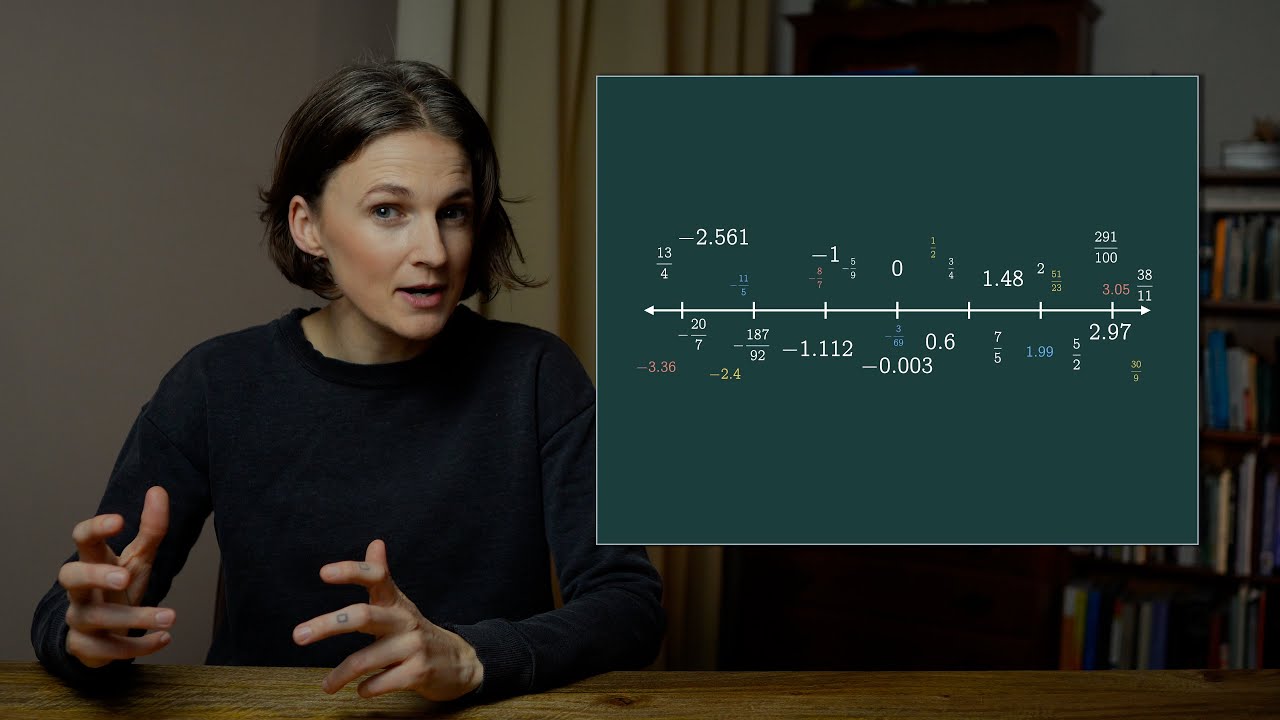
The rational numbers are not so... "rational". (Yes, yes, I know: The name rational comes from ratio — they're the ratios of whole numbers. The word rational has a second meaning. We're playing with that here.)

________________

Timestamps:
0:00 Intro
0:39 Everywhere
2:09 But Nowhere

_______________

_______________

Created by Kelsey Houston-Edwards

Support the channel:

[SoopaPop]

I first started watching Infinite Series when I was a math undergrad. I've since finished my doctorate (Math: Numerical Analysis) and been working at a research institute for over a year. So glad to see you still making math youtube videos! So funny, this would have been a mind blow to me back then and now I'm watching it because I'm just bored after work on a Tuesday and don't want to think super hard. Thanks!

[f-th]

OH MY GOD YOU'RE BACK
I'VE WAITED SEVEN YEARS
IMMEDIATE SUBSCRIPTION

[readjordan]

Her and PBS infinite series is an influential part of why i became a math major in the first place. I cant believe theres been 2 years of videos and the algorithm didnt let me know!

[valloway]

You have no idea how much we loved Infinite Series! Years later, I still think about it and how great the three of you were. Please keep making more videos!

[trevorbradley]

This is like Christmas for me.

I missed Infinite Series dearly and didn't know Kelsey had returned to youtube.

And I've been coincidentally obsessed with the density of the reals of late.

[tsalVlog]

omg how did I not find this channel sooner?! I used to watch Infinite Series (and some other PBS channels) and have missed your style of teaching! Glad you're still around!

[sander_bouwhuis]

1. I absolutely love your demeanor.
2. I always use the following explanation when I try to explain this to people:
A rational number is a number which 'ends', i.e., has an INFINITE amount of zeroes after a certain point, or it is a number which has some part repeat infinitely many times.
Now, let's try to construct a rational number by throwing a 10-sided die (with faces 0 through 9):
a) after a certain point, you MUST ONLY throw '0'. Not just a couple of times, but INFINITELY many times. So, the likelihood of that happening is 10^-1 (=1/10) for one zero, 10^-2 (=1/100) for two zeroes, …, 10^-∞ for an infinite amount of zeroes. Therefore, it is simply impossible.
b) after a certain point, you MUST ONLY throw a fixed repeating sequence, e.g., or '123123123123…'. That is equally hard as throwing only zeroes. So, again, we end up with a chance of 10^-∞.
Conclusion: randomly choosing a number and coming up with a rational or natural number is literally impossible in a stochastic process.

[srivatsavakasibhatla]

So happy to see you back, KHE! Always loved your PBS videos, please continue enlightening us on YouTube. Amazing video, Welcome Back!

[LillianRyanUhl]

Hi Kelsey, it's great to see another video come through by you! I remember I started watching you in high school, around when I had taken calc 1 & 2 from a small community college

Your role back with PBS Infinite Series was one of the key inspirations for me to seek out higher education in mathematics, and in a couple weeks I'll be graduating with my MSc in mathematics! Your work was hugely influential in my pursuits, so thank you for continuing on the good work still today :)

[giiga]

Glad to see you back! Your videos really helped me learn Module Lattice Post Quantum crypto for a project I was working on. Thank you!

[nicolasgiuristante]

I never thought I'd miss videos I, more often than not, don't fully understand (I never studied mathematics above high school concepts). Yet here I am and glad you posted again!

[KingZarathus]

I'm loving all the positive reactions from those like myself that loved PBS Infinite Series and are thrilled to see new content from you. Instant subscribe from me and adding this channels video history to my watch later to catch up.

[Kyzyl_Tuva]

Kelsey! So nice to see you back. I’ve missed your videos. So excited to see these.

[faustovrz]

It's nice to see you back!
I really missed Infinite Series.

[uncertainukelele]

I just realised you were the original Infinite Series host. I missed you, and I'm glad you're back!

[queueeeee]

This was basically the intro lecture for real analysis in university.
Love it and love your videos!

[Jop_pop]

Just another person here to say Infinite Series changed my life and I'm so delighted you're making new content - please if possible we'd like to see more from you! Thank you so much

[FoodNCheese]

This was so well produced, nice job. I can imagine how difficult it must be to balance the scale of rigor vs. simplicity in explaining higher math intution. Really well done - I hope the next part touches on the continuum hypothesis!

[A_doe_wasting_her_life]

Omg I instantly recognized you I love you have been doing videos on your own since the pbs series ended. Great stuff :)

[robkb]

So glad to have found your new home on YT, Kelsey. Really enjoyed this, but I see I've got some catching up to do!