filmov
tv
The Product of Two Nonzero Matrices can be the Zero Matrix!

Показать описание
We find a matrix B that satisfies AB=0 where A = [[1, 2][3, 6]].
Subscribe and Ring the 🔔
Discord 🎮
Reddit 👽
PLAYLISTS 🎵 :
Subscribe and Ring the 🔔
Discord 🎮
Reddit 👽
PLAYLISTS 🎵 :
The Product of Two Nonzero Matrices can be the Zero Matrix!
If the dot product of two nonzero vectors is zero, the vectors must be perpendicular to each other.
Explain why the degree of the product of two nonzero polynomials equals the sum of their degrees.
If the scalar product of two nonzero vectors is zero, what can you conclude about their relative di…...
(Any non-zero number)⁰ = ? | Fun Math | Don't Memorise
Is Product of two nonzero matrices is a Zero Matrix??/Matrices/Part11/#class12maths
Cross product formulas definitions explanations examples vector product of two nonzero vectors
If product of two nonzero matrix ( matrices ) is zero matrix then they are singular matrices
The product of any nonzero rational number and any irrational number is irrational
The Vector Dot Product
Geometrically Defining the Cross Product | Multivariable Calculus
Angle between vectors leads to defining the Dot Product | Multivariable Calculus
What is known about θ, the angle between two nonzero vectors u and v, under each condition (s…
If θis the angle between two nonzero vectors 𝐮 and 𝐯, then cos θ= _…
How to find the Angle between Vectors
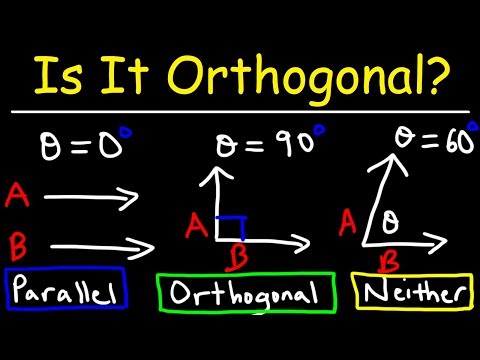
Are The Two Vectors Parallel, Orthogonal, or Neither?
Dot and cross product comparison/intuition | Vectors and spaces | Linear Algebra | Khan Academy
Estimating Products | MathHelp.com
The real world applications of the dot product
Proof that rational times irrational is irrational | Algebra I | Khan Academy
Vector Projections
Cross product introduction | Vectors and spaces | Linear Algebra | Khan Academy
Proof: Relationship between cross product and sin of angle | Linear Algebra | Khan Academy
Find Perpendicular Vectors in R3 with Dot Product
Комментарии
 0:03:36
0:03:36
 0:00:30
0:00:30
 0:00:33
0:00:33
 0:00:33
0:00:33
 0:00:55
0:00:55
 0:03:57
0:03:57
 0:12:08
0:12:08
 0:04:33
0:04:33
 0:10:22
0:10:22
 0:06:59
0:06:59
 0:05:13
0:05:13
 0:06:11
0:06:11
 0:00:33
0:00:33
 0:00:33
0:00:33
 0:05:44
0:05:44
 0:11:49
0:11:49
 0:19:14
0:19:14
 0:02:00
0:02:00
 0:12:49
0:12:49
 0:03:15
0:03:15
 0:06:12
0:06:12
 0:15:47
0:15:47
 0:18:09
0:18:09
 0:06:21
0:06:21