Lecture 4: The Open Mapping Theorem and the Closed Graph Theorem

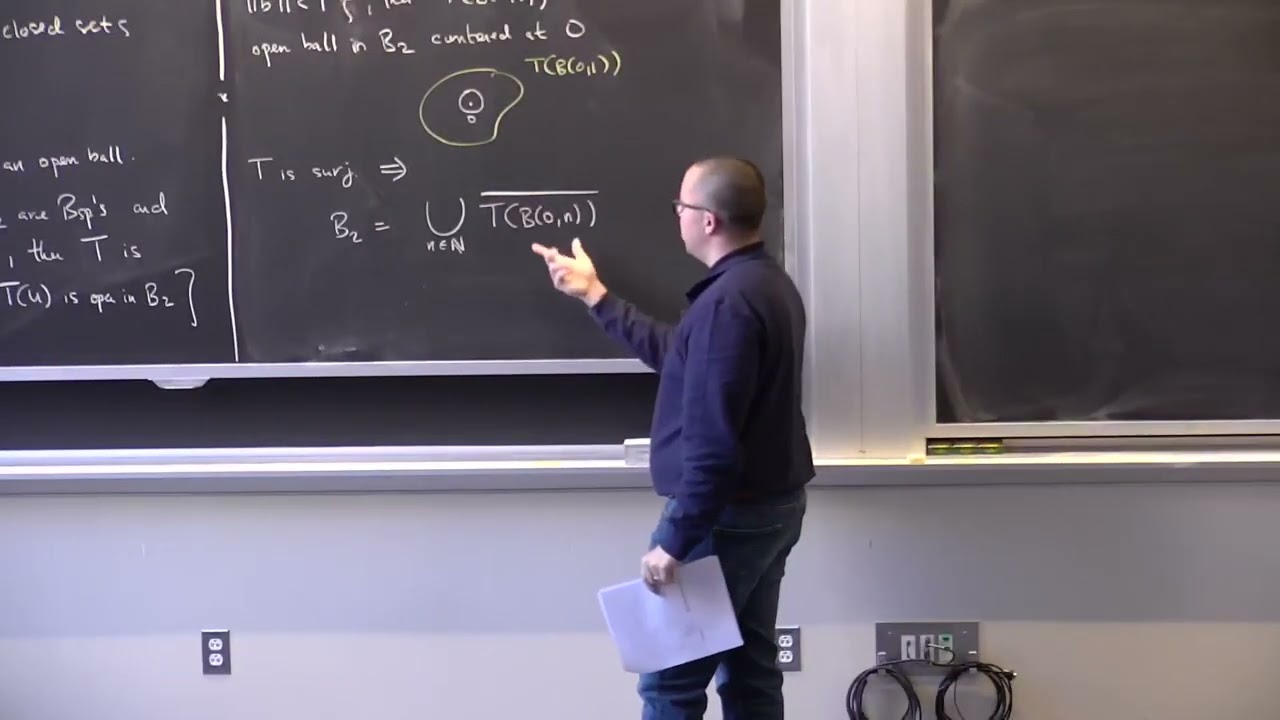
preview_player
Показать описание
MIT 18.102 Introduction to Functional Analysis, Spring 2021
Instructor: Dr. Casey Rodriguez

We prove two more fundamental “theorems with names” as Casey puts it: the Open Mapping Theorem and the Closed Graph Theorem. We conclude with the notion of a Hamel basis for a vector space (finite or infinite dimensional).

License: Creative Commons BY-NC-SA

  1. MIT OpenCourseWare
  2. Closed Graph Theorem
  3. Hamel basis
  4. Open Mapping Theorem
  5. Zorn’s lemma
Рекомендации по теме
Lecture 4: The 1:14:58

Lecture 4: The Open Mapping Theorem and the Closed Graph Theorem

Lectures 34: 4.12 0:15:20

Lectures 34: 4.12 Open Mapping Theorem

4.2 - Open 0:31:10

4.2 - Open mapping and closed graph theorems

Functional Analysis 26 0:05:38

Functional Analysis 26 | Open Mapping Theorem

Lecture 19 (Part 0:24:29

Lecture 19 (Part 4): Open mapping theorem proof (continued)

Doctorate program: Functional 0:46:36

Doctorate program: Functional Analysis - Lecture 30: Open map principle.

Lecture 4: Aircraft 0:49:51

Lecture 4: Aircraft Systems

Lecture 26: Open 0:48:36

Lecture 26: Open map, closed map and connectedness

Computer Architecture - 2:47:01

Computer Architecture - Lecture 11: Memory Controllers: Service Quality and Performance (Fall 2024)

Lecture 19 (Part 0:30:27

Lecture 19 (Part 1): Open Mapping Theorem and some of its consequences

Proof of Lemma 0:07:24

Proof of Lemma 1 of Open Mapping Theorem part-4

Lecture 4: Expectations, 1:20:07

Lecture 4: Expectations, Momentum, and Uncertainty

Complex Variables (Lecture 0:57:37

Complex Variables (Lecture 4): Properties of Holomorphic Functions

Open mapping, inverse 1:14:45

Open mapping, inverse mapping and closed graph theorems

Lecture 8.2 - 0:51:49

Lecture 8.2 - Open mapping theorem

Open Mapping/ Continuity 0:12:27

Open Mapping/ Continuity and homeomorphism/ Topology/ Mathematics for M.A, M.sc by Vibhor tyagi

Open Mapping Theorem 0:48:19

Open Mapping Theorem (Nonlinear Version)

Complex Variables (Lecture 1:21:13

Complex Variables (Lecture 21): The Open Mapping and Maximum Modulus Theorems

IIT Bombay Lecture 0:00:12

IIT Bombay Lecture Hall | IIT Bombay Motivation | #shorts #ytshorts #iit

The open mapping 0:24:20

The open mapping theorem

Proof of Lemma 0:13:09

Proof of Lemma 1 of Open Mapping Theorem part-3

Proof of Lemma 0:07:39

Proof of Lemma 1 of Open Mapping Theorem part-1

Homotopy Theory Lecture 1:27:38

Homotopy Theory Lecture 4

Multivariable Calculus Lecture 0:48:03

Multivariable Calculus Lecture 4 - Oxford Mathematics 1st Year Student Lecture

Комментарии
Автор

"So let's continue with the 'big-name theorems' or the 'theorems with big names' or the 'big theorems with names'", absolutely hilarious!

travischapman
Автор

Thanks mit for providing high quality education

coreconceptclasses
Автор

Open mapping theorem is the most used result from functional analysis

briang.valentine
Автор

35:37 End of proof to open mapping theorem
57:21 End of proof to closed graph theorem

oldPrince
Автор

At 35:25, you mark the proof of the open mapping theorem as complete. I'm not sure that it is. Maybe it's my own ignorance. I've never taken any analysis or topology courses. I've only watched some lectures on YouTube, including a few from your course on real analysis.

It seems to me that you've shown that T(U) contains an open ball, namely B(b2, epsilon*delta). But I don't see how this implies that T(U) is open (I'm assuming you mean open with respect to the topology on B2 induced by the norm). This is especially confusing for me since, in Baire's theorem, it was shown that at least one of those *closed* subsets (given by the conditions in the theorem) contains an open ball. Am I missing something?

zn
Автор

I remember when the 4 color was a lived controversy.

SSNewberry
Автор

When would any of this be used in life?

joenissan